Imagine your local newspaper is organizing a contest in which they’d like to find the “cutest“ puppy in the region.
The rules of the contest are simple: Residents in your area vote for one of the three puppies in the contest who they think is the cutest. As most contests go, the puppy who receives the most votes wins! But there’s a twist, the residents who voted for the wining puppy are also eligible for some sort of prize. In short, they are rewarded for guessing correctly!
You acknowledge this attempt by the publication to sell ad space & papers, but it has caught your attention. After reading the rules of the game, you go back and forth between a few of your favorite puppies (we will call them Puppy #1, #2, and #3).
You could pick your favorite puppy, #1. However, it dawns on you that this may not be the best way to go about this contest. Therefore, you soon devise a strategy.
If others have different opinions of "cuteness," then you will have a low chance to win a prize. Voting for Puppy #1 is pointless, even if you think it is the cutest. The most rational decision would not be to vote for your top choice (Puppy #1), but the puppy that you think others would vote for (Puppy #2). However, this poses a deeper level of thinking - maybe the other residents of your town are thinking along the same lines as you, and they think that their fellow townspeople would not vote for Puppy #2, but rather Puppy #3.
You have now found yourself in a dilemma, which can be best explained by MobLab’s Keynesian Beauty Contest Game.
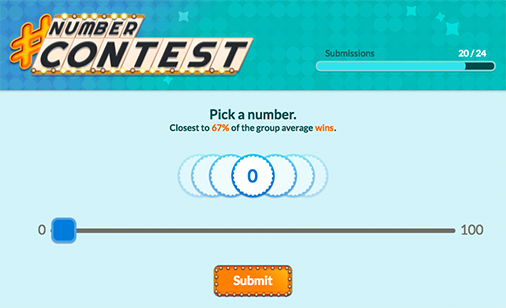
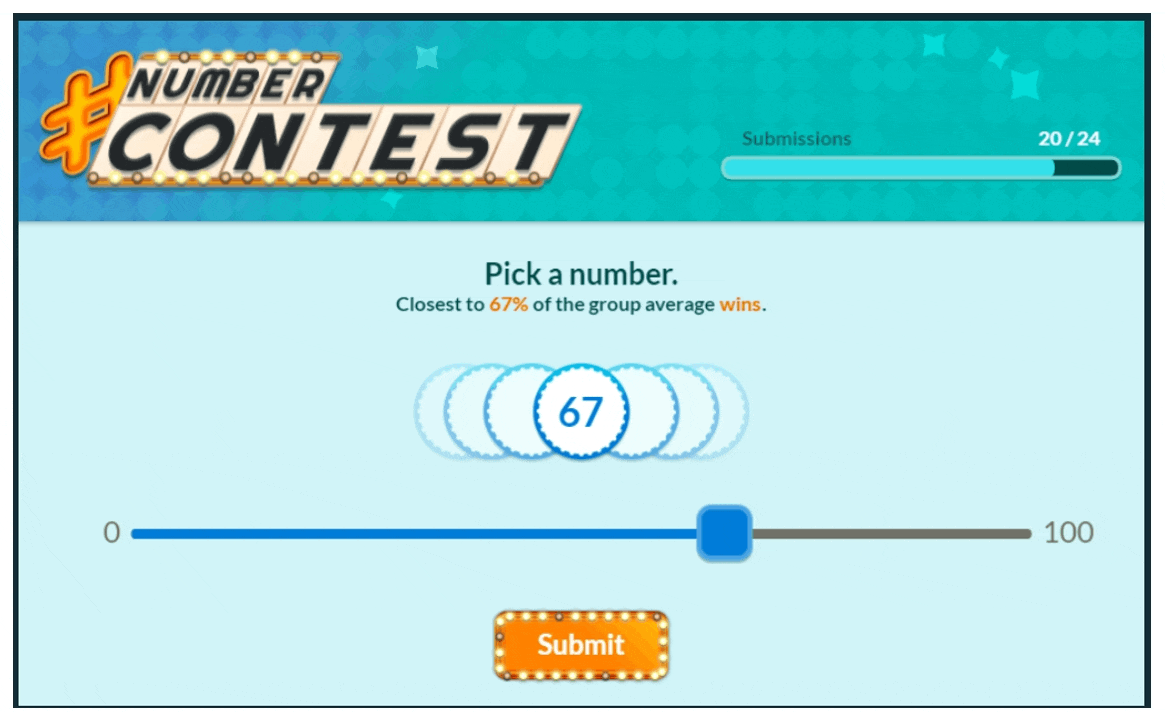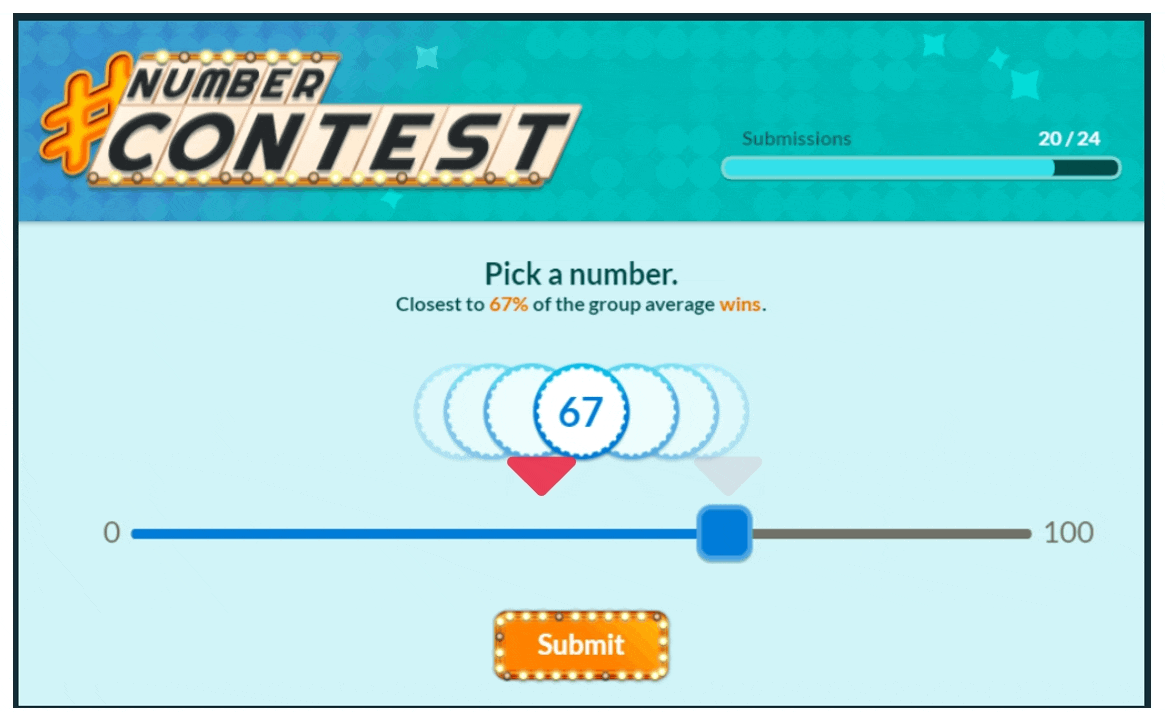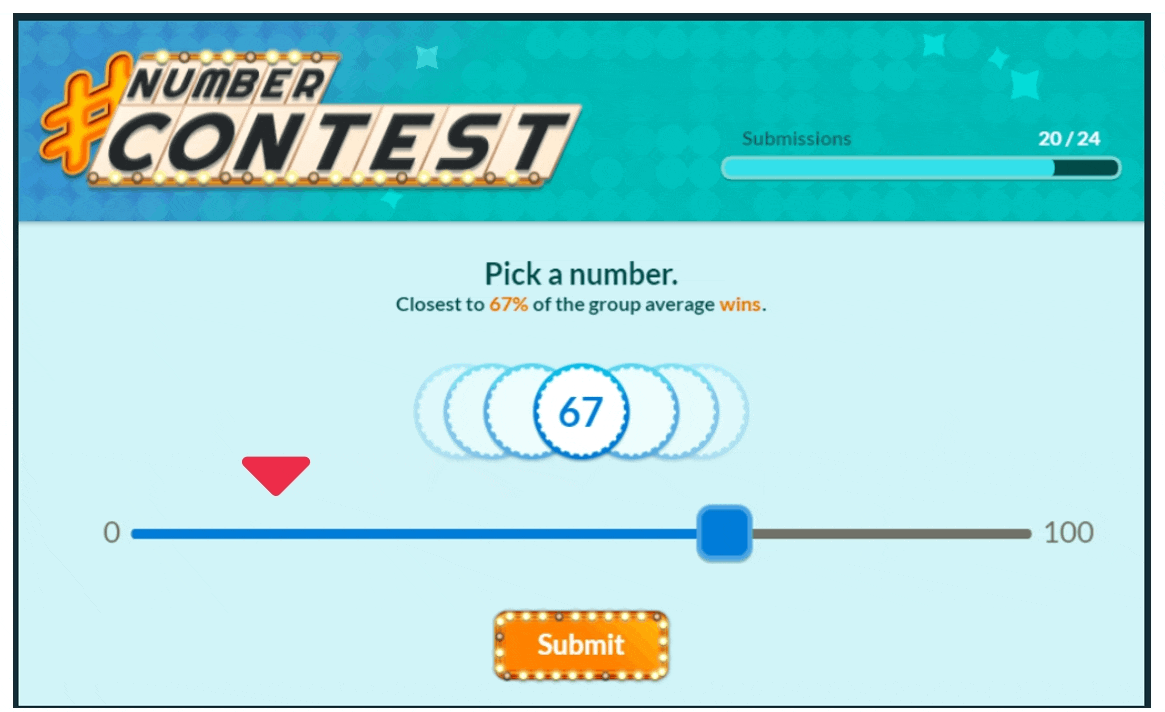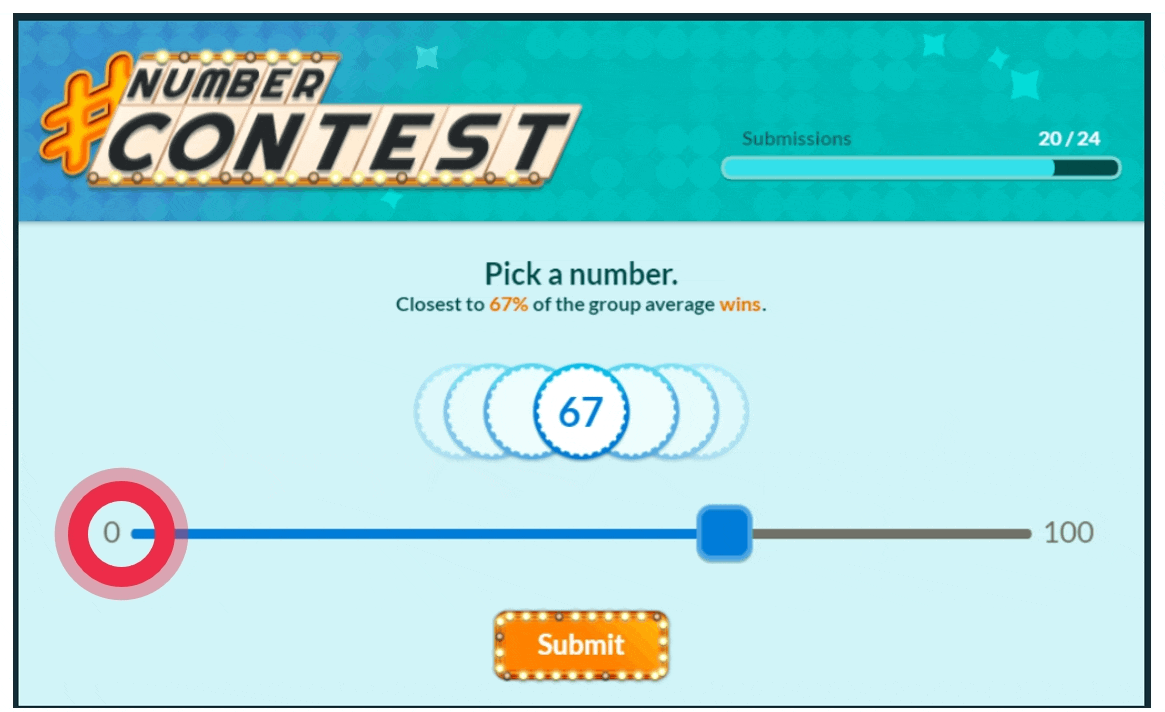
Game Screen of the MobLab Keynesian Beauty Contest
MobLab’s version of the beauty contest has simple rules. Students pick an integer from 0-100 with the goal of picking the number that is closest to 67% (2/3) of the average of all guesses.
This game covers a few learning objectives including: Strategic Thought & Iterated Dominance.
Let’s start from the beginning. A student, Alex, quickly realizes that if the rest of their class chooses 100, the winning guess would be to choose 67 (2/3 of the average of all guesses). Alex thinks the winning answer has to be 67 or less. Therefore, Alex contemplates selecting 67 for a split second. However, they soon realize that maybe the rest of the class is thinking the same thing! Alex goes one level deeper “If the rest of the class is going to choose 67 - then I will choose 45 (roughly 67% of 67).”
In a large class of 100 students, Alex cannot assume they are the only one who has gone to this level of thinking. How far does this thought process go? Continuing down that same level of thinking, all numbers greater than 0 are eliminated through iterated elimination of weakly dominated strategies. Theoretically, Alex and their classmates all choose 0, as they continually dive deeper into their strategy.
How is this relevant in your economics concepts course? Let’s connect our newspaper example with the stock market. Assume that you think the shares of Company X will fall in the coming months. Fundamentally, you believe we are in a bubble! As any good investor, you have to take into account what others are doing! If you think that others think that prices will remain stable, it is rational to hold onto those shares. Going one level deeper: regardless of what you think, if the majority believes that OTHERS believe that share prices will increase - it would be rational to participate in this bubble as you stand to benefit from higher share prices (deep breath - a lot of levels). The same principle can be applied to the recent rise of NFTs (non-fungible tokens).
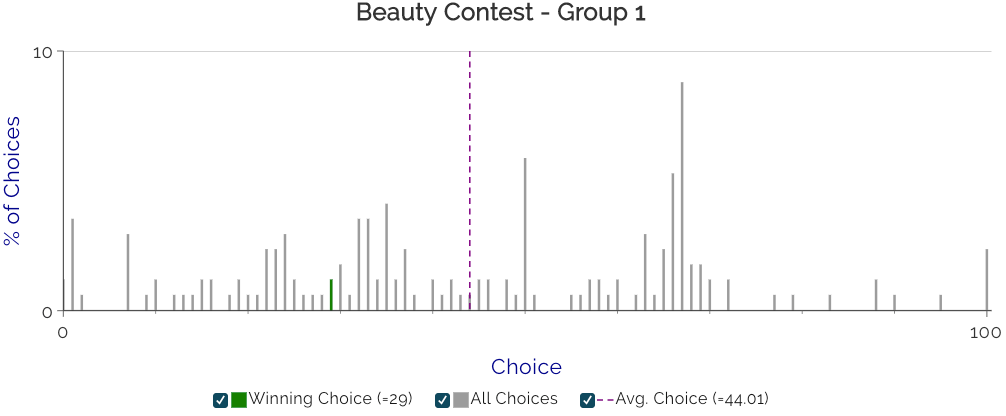
Below are some sample results - showing the distribution of choices. In this particular game, the average choice was 44.01 - and therefore, the closest to 67% of this was 29. This game is a common demonstration in game theory & macroeconomics classes, where even economics graduate students do not guess 0!
Games can be a great way to keep your students engaged in economic concepts, especially when coupled with a debrief of the results from the class. Want to learn more about bringing economics games into the classroom? Please contact our team for more information!
The rules of the contest are simple: Residents in your area vote for one of the three puppies in the contest who they think is the cutest. As most contests go, the puppy who receives the most votes wins! But there’s a twist, the residents who voted for the wining puppy are also eligible for some sort of prize. In short, they are rewarded for guessing correctly!
You acknowledge this attempt by the publication to sell ad space & papers, but it has caught your attention. After reading the rules of the game, you go back and forth between a few of your favorite puppies (we will call them Puppy #1, #2, and #3).
You could pick your favorite puppy, #1. However, it dawns on you that this may not be the best way to go about this contest. Therefore, you soon devise a strategy.
If others have different opinions of "cuteness," then you will have a low chance to win a prize. Voting for Puppy #1 is pointless, even if you think it is the cutest. The most rational decision would not be to vote for your top choice (Puppy #1), but the puppy that you think others would vote for (Puppy #2). However, this poses a deeper level of thinking - maybe the other residents of your town are thinking along the same lines as you, and they think that their fellow townspeople would not vote for Puppy #2, but rather Puppy #3.
You have now found yourself in a dilemma, which can be best explained by MobLab’s Keynesian Beauty Contest Game.

Game Screen of the MobLab Keynesian Beauty Contest
This game covers a few learning objectives including: Strategic Thought & Iterated Dominance.
Let’s start from the beginning. A student, Alex, quickly realizes that if the rest of their class chooses 100, the winning guess would be to choose 67 (2/3 of the average of all guesses). Alex thinks the winning answer has to be 67 or less. Therefore, Alex contemplates selecting 67 for a split second. However, they soon realize that maybe the rest of the class is thinking the same thing! Alex goes one level deeper “If the rest of the class is going to choose 67 - then I will choose 45 (roughly 67% of 67).”
In a large class of 100 students, Alex cannot assume they are the only one who has gone to this level of thinking. How far does this thought process go? Continuing down that same level of thinking, all numbers greater than 0 are eliminated through iterated elimination of weakly dominated strategies. Theoretically, Alex and their classmates all choose 0, as they continually dive deeper into their strategy.

Below are some sample results - showing the distribution of choices. In this particular game, the average choice was 44.01 - and therefore, the closest to 67% of this was 29. This game is a common demonstration in game theory & macroeconomics classes, where even economics graduate students do not guess 0!


