With the first Presidential Debates tonight, the election season is reaching a fever pitch. There were several places I could go with the election cycle. For example, Steve Brams’ piece on how game theory helps explain Trump's strategies. However, it seems an appropriate time to write about our Two Candidate Election Game.
In this game students are politicians seeking to win an election. The default parameters structure the game as follows:
There are two candidates that make a choice about how to locate on a line that ranges from 0 to 100. An odd number of voters (in the default 51) are drawn from a uniform distribution around the median voter (default 50). Each candidate has an opportunity to “poll” twice. A poll reveals the following to the student: Given that you chose to locate at position X and your opponent chose to locate at Y the vote outcome was the following:
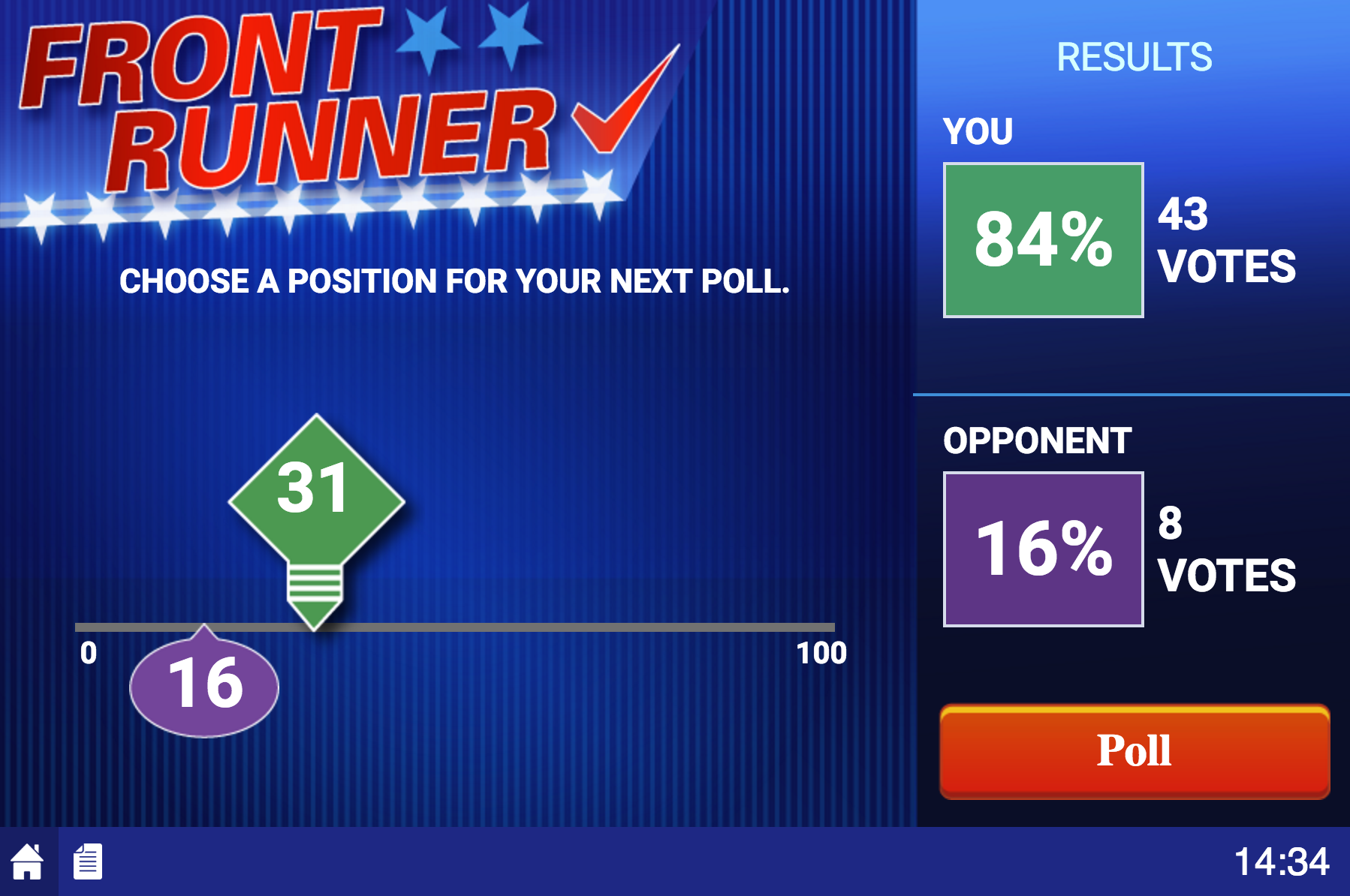
Students do the poll again. Then, after the polling feedback each chooses a “policy position”. With the default parameters the payoffs are based on “winner take all” where the winner receives 100 and the loser receives 0.
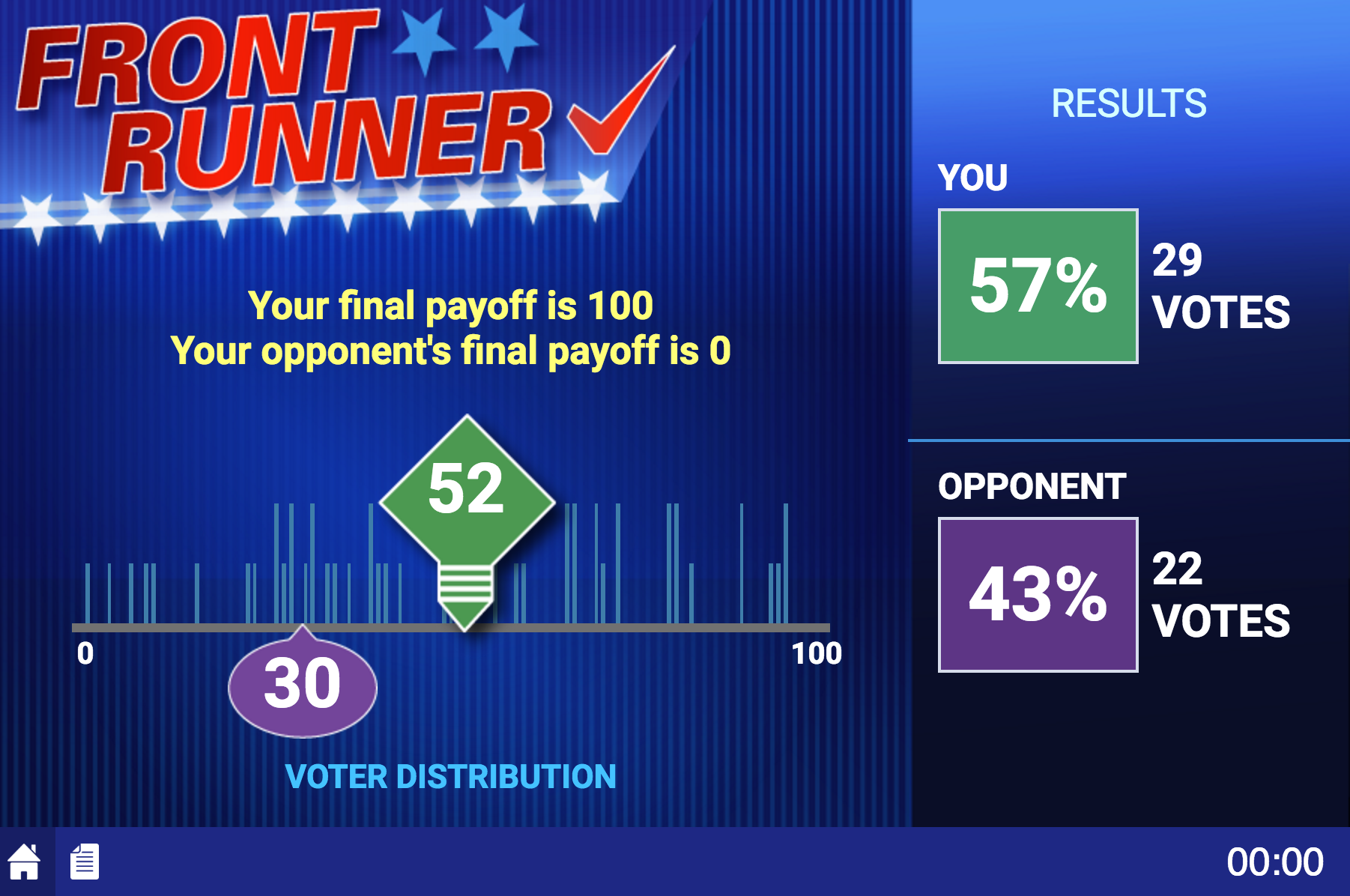
Now we turn to some manipulations within the game:
Want to learn more about bringing interactive games into the Political Science classroom? Please contact our team for more information!