Introduction
Your students may not be familiar with the 1970s show “Let’s Make a Deal,” yet the simple decision problem with the three doors named after the show’s host, Monty Hall, remains a popular narrative for introducing Bayes' Rule and conditional probability. MobLab’s Monty Hall game will present your students with the decision problem and gather their answers and give you the results immediately during your lecture.
The Decision Problem
You are given the choice of winning the prize behind one of three doors: behind one door is a car; behind the others, goats. You pick a door, say No. 3. Before revealing your door, the host opens one of the doors not selected, say No. 2, which has a goat. He then asks you, "Do you want to change your pick to door No. 1?" Is it to your advantage to switch your choice?
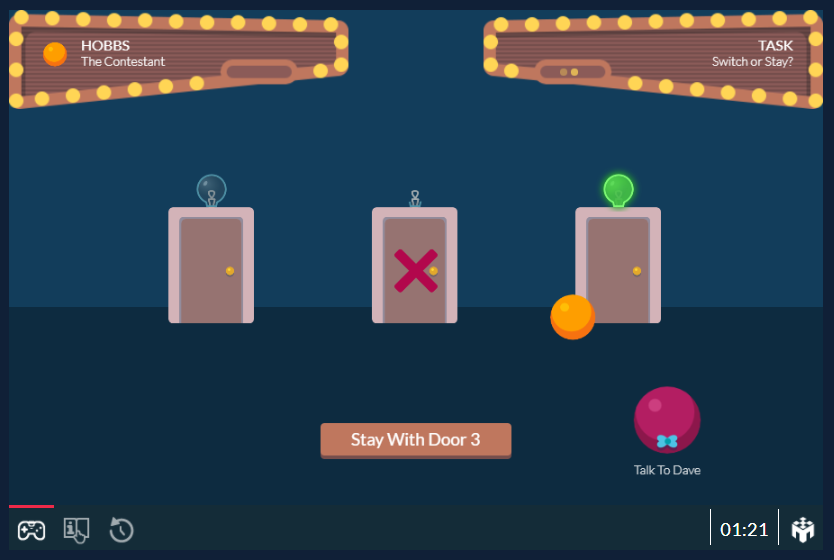
Figure 1. Monty Hall Game Interface
Bayes' RuleBayes' Rule allows us to update probability when we get new information (conditional probability) and can help us to answer this question. Let’s define A as the event that the car is behind door No. 3, and B as the event that a goat is shown behind door No. 2. So what is the probability, P(A|B), that a car is behind door No. 1, given that the host showed a goat behind door No. 2? Bayes’ Rule tells us that it is equal to the probability of A and B occurring divided by the probability of B occurring:

We know that the initial probability of having a car is the same for all thee doors: P(A) = 1⁄3 .
After our initial pick, the probability of Monty opening either of the remaining doors is equal: P(B) = 1⁄2 .
Now we can calculate P(A,B):
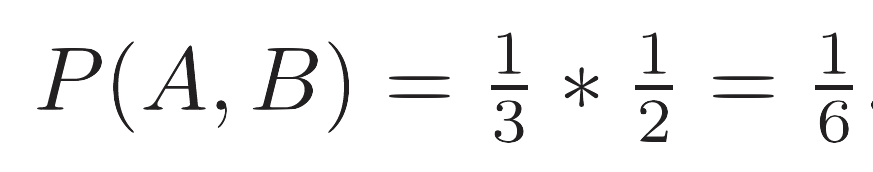
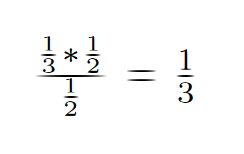
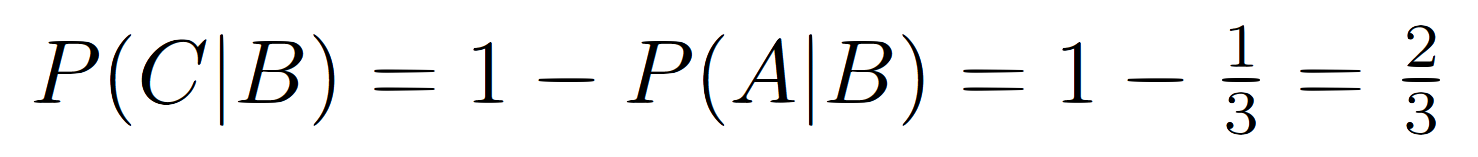
In other words, it is twice as likely that the car is being behind the other door. This implies that the best strategy is to always switch to the other door when asked by the host.
Conclusion
With MobLab’s Monty Hall game, a seemingly complicated economics concept like Bayes’ Rule, is broken down for students in an intuitive and playful way. We offer the same approach for various further topics from business to economics. Check out our game catalog to see how MobLab fits into your class.
Switching to MobLab's economics games is always a winning strategy! Get in touch with our team! We are eager to set it up for your class.
Your students may not be familiar with the 1970s show “Let’s Make a Deal,” yet the simple decision problem with the three doors named after the show’s host, Monty Hall, remains a popular narrative for introducing Bayes' Rule and conditional probability. MobLab’s Monty Hall game will present your students with the decision problem and gather their answers and give you the results immediately during your lecture.
The Decision Problem
You are given the choice of winning the prize behind one of three doors: behind one door is a car; behind the others, goats. You pick a door, say No. 3. Before revealing your door, the host opens one of the doors not selected, say No. 2, which has a goat. He then asks you, "Do you want to change your pick to door No. 1?" Is it to your advantage to switch your choice?

Figure 1. Monty Hall Game Interface
Bayes' Rule

We know that the initial probability of having a car is the same for all thee doors: P(A) = 1⁄3 .
After our initial pick, the probability of Monty opening either of the remaining doors is equal: P(B) = 1⁄2 .
Now we can calculate P(A,B):
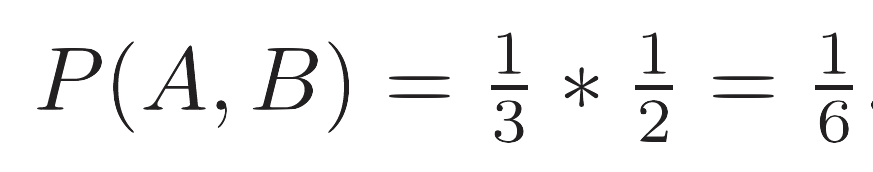
By applying Bayes' Rule, we get P(A,B)/P(B) as the probability of the car being behind our initial pick:
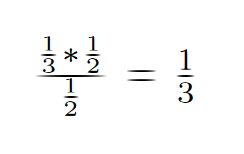
Consequently,the probability that the car is behind the other door (our example No. 1) given that host has showed a goat behind door No. 2 is:
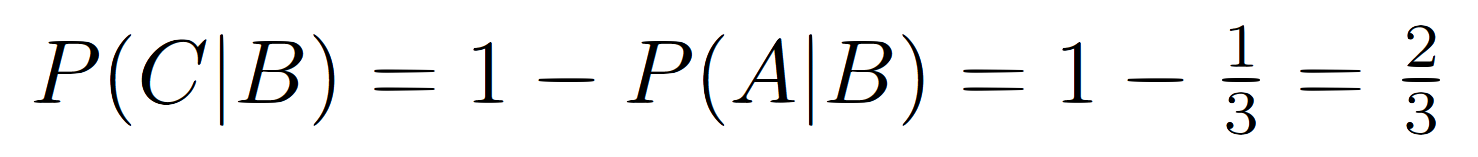
In other words, it is twice as likely that the car is being behind the other door. This implies that the best strategy is to always switch to the other door when asked by the host.
MobLab’s Extension to Highlight the Underlying Intuition
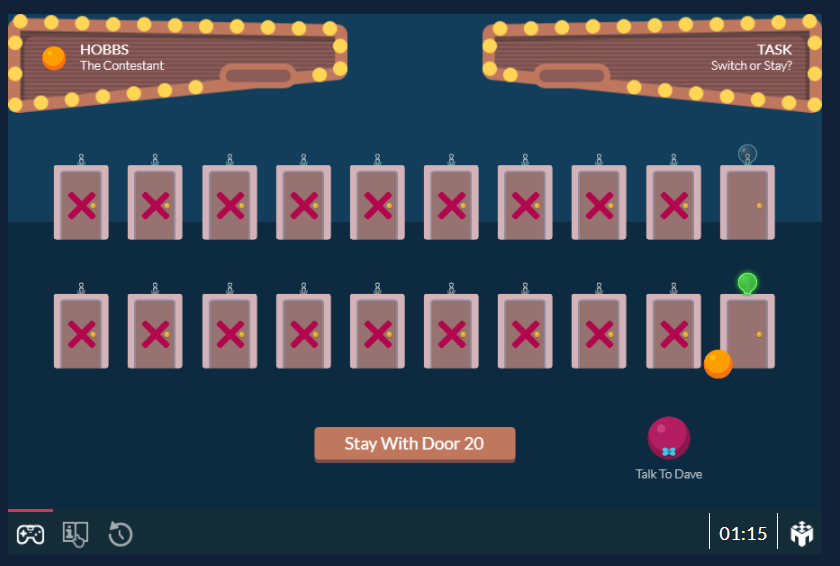
Bayes’ Rule may not necessarily look intuitive at first glance. This is where MobLab’s Monty Hall game comes into play. We recommend you first play the game with the traditional setup of three doors. Then, you let students replay the game, this time facing 20 doors. After making their initial choice, our magenta host, Dave, reveals 18 doors which do not have the car, or in our version of the game, a yellow gem. Do you want to stick with your initial choice or switch to the one remaining door that was not opened by Dave? This approach helps understanding the problem by thinking about it as the probability being narrowed down to the remaining door. The probability of your first guess being correct (1/20) is much smaller than the probability of winning if you switch doors (19/20). Gaining an intuition for Bayes’ Rule will serve your students in all its everyday life appearances, ranging from medical testing over insurance contracts to investment strategies.
Bayes’ Rule may not necessarily look intuitive at first glance. This is where MobLab’s Monty Hall game comes into play. We recommend you first play the game with the traditional setup of three doors. Then, you let students replay the game, this time facing 20 doors. After making their initial choice, our magenta host, Dave, reveals 18 doors which do not have the car, or in our version of the game, a yellow gem. Do you want to stick with your initial choice or switch to the one remaining door that was not opened by Dave? This approach helps understanding the problem by thinking about it as the probability being narrowed down to the remaining door. The probability of your first guess being correct (1/20) is much smaller than the probability of winning if you switch doors (19/20). Gaining an intuition for Bayes’ Rule will serve your students in all its everyday life appearances, ranging from medical testing over insurance contracts to investment strategies.

Figure 2. Monty Hall - Game with 20 Doors
Conclusion
With MobLab’s Monty Hall game, a seemingly complicated economics concept like Bayes’ Rule, is broken down for students in an intuitive and playful way. We offer the same approach for various further topics from business to economics. Check out our game catalog to see how MobLab fits into your class.
Switching to MobLab's economics games is always a winning strategy! Get in touch with our team! We are eager to set it up for your class.

