In October I had the good pleasure of demonstrating MobLab to a 400 student class at UNC. That day students were learning about monopolistic competition and one component of the discussion was collusion. Naturally, we decided to play the Prisoner's Dilemma (PD) --- that old workhorse for studying the conditions under which cooperation is more or less likely to occur. The students were really excited about doing classroom experiments. I even had students shaking my hand and telling me so in advance of class!
We played a sequence of three repeated PD. The first session was a five round game with fixed partners. In the second session students were randomly rematched with someone else for a five round game with communication.
In the left panel you can see the game begins with more cooperation than defection 28.6% C/C (Green) v. 21% D/D (Red). However, C/C declines to 8.6% while D/D climbs to 56% by the final round. In the right panel with communication C/C starts at 46.5% and by the fourth round maintains at 44.4%. In the final round there is an end-game effect to C/C of 17%. In this case the D/D equilibrium climbs across time from 15.1% to 45.7% With such a change in cooperation rates it definitely calls to mind that old quote from the Wealth of Nations where Adam Smith writes,
“I’m going to trust you on this” “i gotta know if ur trustworthy” “If you pick D one time I will pick D every time and we will both lose” “you suckkkk” “Lol I gotta do what I gotta do to get the victory” “YOu do realize we get the most if we both choose C, right?”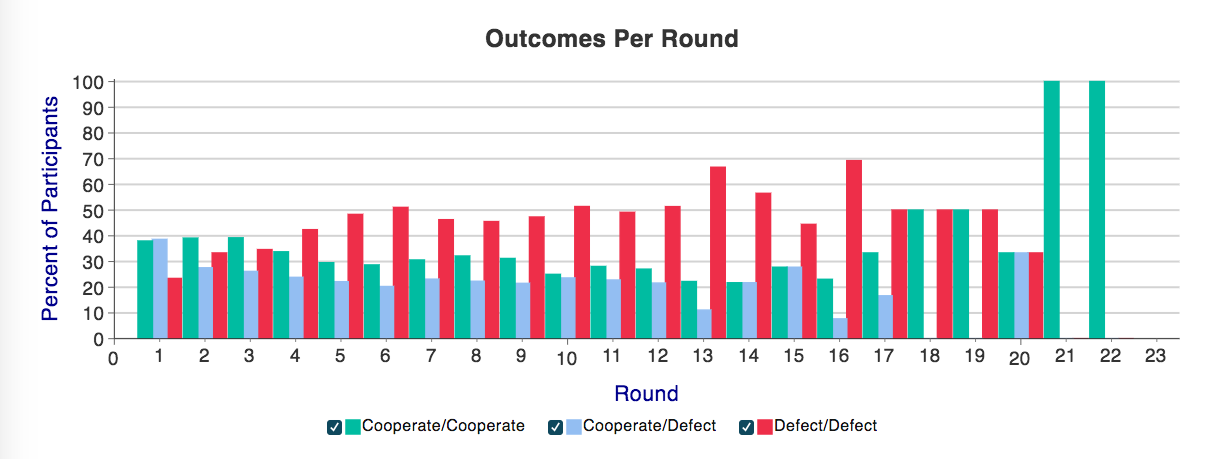 
In subsequent in-class examples the instructor was able to build on student's improved understanding of the conventions of the payoff matrix and strategic considerations that lead to the Nash Equilibrium. It was a blast! I had a lot of fun and the students got a lot out of it.
Check out our blog for more tips on the Prisoner's Dilemma matrix game. Want to learn more about our online economics games? Get in touch and we would be happy to give you a personalized tour of the MobLab economics games platform.
We played a sequence of three repeated PD. The first session was a five round game with fixed partners. In the second session students were randomly rematched with someone else for a five round game with communication.
In the left panel you can see the game begins with more cooperation than defection 28.6% C/C (Green) v. 21% D/D (Red). However, C/C declines to 8.6% while D/D climbs to 56% by the final round. In the right panel with communication C/C starts at 46.5% and by the fourth round maintains at 44.4%. In the final round there is an end-game effect to C/C of 17%. In this case the D/D equilibrium climbs across time from 15.1% to 45.7% With such a change in cooperation rates it definitely calls to mind that old quote from the Wealth of Nations where Adam Smith writes,"People of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the public, or in some contrivance to raise prices."Finally, after two sour experiences with partners in the PD experiment we randomly rematched students with new partners. This time we ran a PD with chat and indefinite repetition. With indefinite repetition and communication 78 out of 161 groups made it through the tenth round. After the tenth round observations start to drop significantly. Despite people learning from the broken promises or “cheap talk” in the PD with communication cooperation still started out rather high. C/C started at 38% in the first round. By the tenth round C/C was 25%, much higher than cooperation in final round of the game with the finite ending. As with the previous games, D/D climbs across time from 23.4% in the first round to 51.4% by the tenth round. The .csv data files contain chat transcripts which are usually an absolute gold mine. Some examples:
In subsequent in-class examples the instructor was able to build on student's improved understanding of the conventions of the payoff matrix and strategic considerations that lead to the Nash Equilibrium. It was a blast! I had a lot of fun and the students got a lot out of it.Check out our blog for more tips on the Prisoner's Dilemma matrix game. Want to learn more about our online economics games? Get in touch and we would be happy to give you a personalized tour of the MobLab economics games platform.