Welcome to part two of our series on pulling back our curtains at MobLab to give you a peek under the hood. As with our first post on Competitive Market, our goal here is to share some observations that we have learned from running analytics on our games. We continue to be excited by seeing the results of live data from our games against economics theories. Today we want to dive deeper into another one of our most popular games, Push & Pull.
Push & Pull - Set Up
The Push & Pull game is an adaptation of the prisoner’s dilemma by Jim Andreoni & Hal Varian (1999). Instead of a classic matrix game, students are presented with two cards that they can play in which they either push a relatively higher reward to the other player or pull a relatively lower reward to themselves.
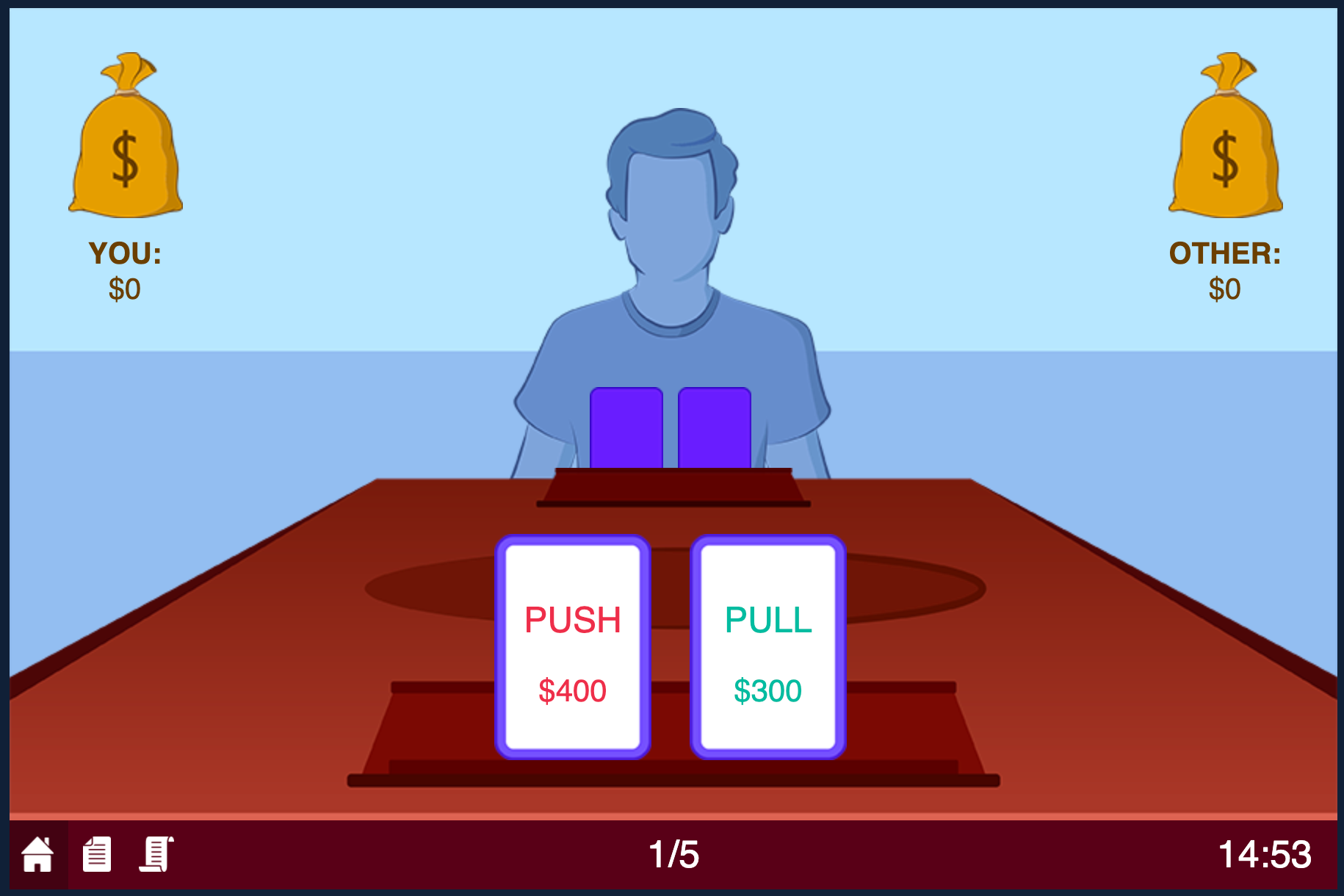
Figure 1. Game Interface with Action Set
The keen observer notes already that this game is the prisoner’s dilemma in a different framing. The action sets and payoff structure are analogous to those of the prisoner’s dilemma. As such, the pushing is the equivalent of the cooperate action and the pulling is the defect action.
The Problem
The prisoner’s dilemma occurs when two (or more) actors are faced with the same two choices: one choice leads to an overall better payoff for the group and each individual member (e.g. 2 * $400 for each if both Push); the other, actors have an individual incentive to defect (e.g. 2 * $300 for each) since they are individually better off to deviate regardless of whether the other actor cooperates or defects. This logic depicts many strategic situations such as arms races, doping in sports competitions, advertisement bidding, etc.
The interesting question is how do we overcome this dilemma?
Solution I - Repeated Interaction
One commonly proposed solution to this issue is repeated interaction. When trying to prevent an arms race, you can think of countries trying to tie themselves together in trade agreements, mutual cultural exchange, etc. to facilitate this kind of repeated interaction. However, theorists point out that repeated interaction in and of itself is not sufficient to sustain cooperation. Why is this? Well, if we suppose that the interactions last for say 5 rounds, the last round can be thought of as a simple one-round interaction since it is known that there is no next round taking place. That means the participants are incentivized to choose to defect. Given this knowledge, they should also defect in round 4 and you can see that this logic applies all the way to the first interaction, and the hope of cooperation is lost. But how does this theory hold up against the data in our treasure chest? We took all games which were played for 5 rounds and analyzed the mutual cooperation at the group level. That gives us N = 9004 observations.
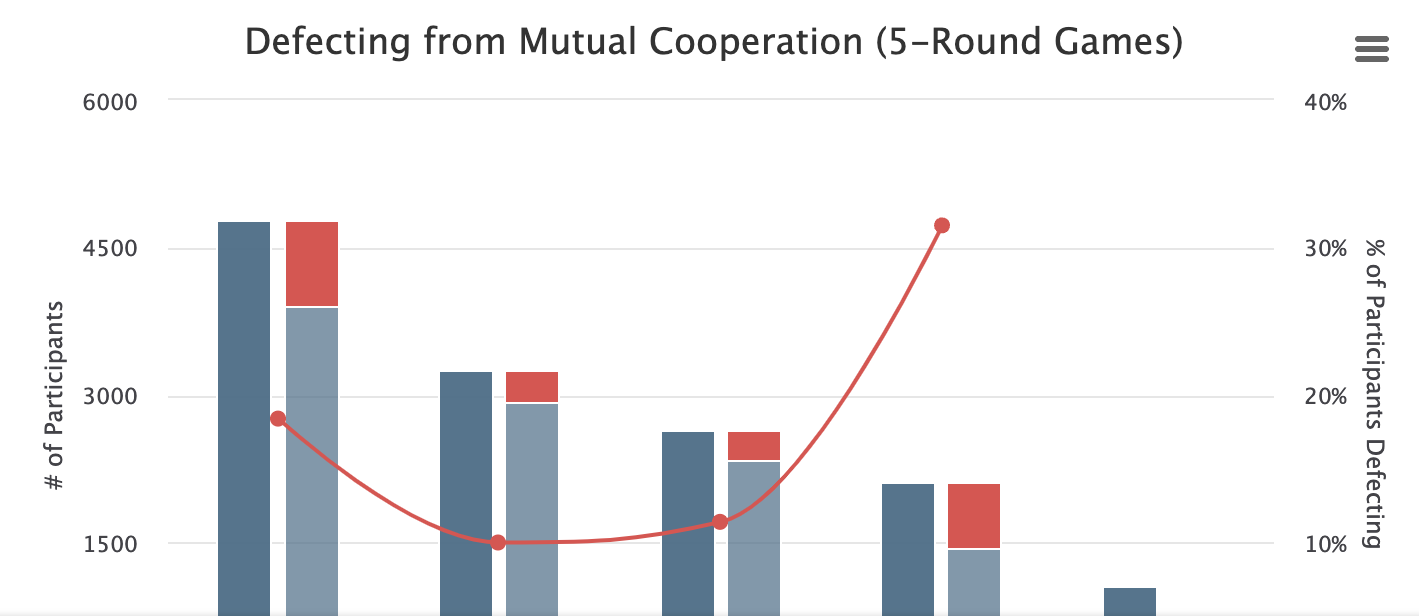
Figure 2. Definitely Repeated Interaction
It turns out that our data does not show exactly the pattern theory predicts but tells a slightly different story. About 30% of participants manage to achieve mutual cooperation in the first round despite the theory predicting that no cooperation should take place. The theory is right though in predicting that this cooperation is largely not sustainable and drops to less than 10% of groups sustaining mutual cooperation in round 5. Empirically, we observe an interesting phenomenon where this drop off is most pronounced in the last round (31.5%). This has been observed by others before and has been called the “last round effect.” It suggests that the theory partially predicts the behavior. Regardless though, it is evident that this repetition is not able to produce mutually beneficial cooperation.
Solution II - Indefinite Repetition
But what if the actors don’t know when the repeated interaction will end? That is, if they do not know when the interaction with the other actors will end, they might be able to sustain cooperation. The logic derives from the fact that if the actors do not know when the interaction will end, the gain from momentarily defecting is outweighed by the potential loss of no future cooperation. Based on this, we would predict that we should observe higher levels of cooperation. We were able to retrieve N=1054 pairings from our database that played this game for at 3 rounds in the definite repetition treatment and N=3372 pairings in the indefinitely repetition treatment (50% probability that the game continues after round 3). Let’s look at what we can find concerning defection and cooperation.
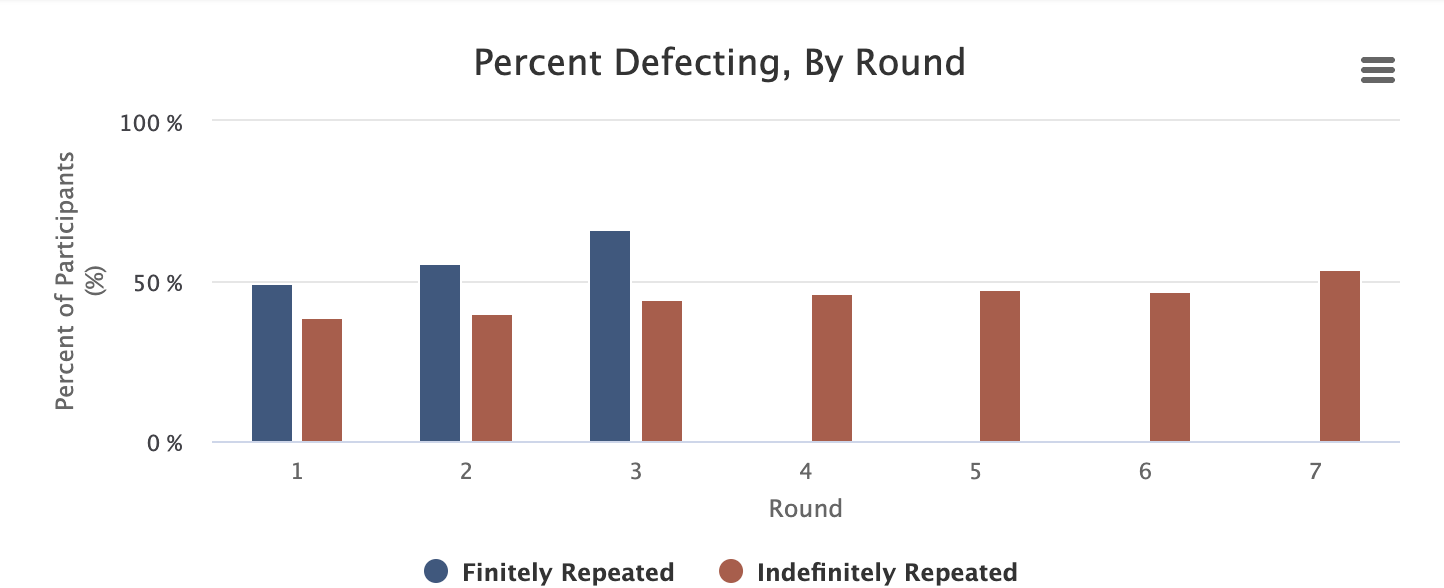
Figure 3. Percent Defect, By Round
As we can see, the levels of defection are higher in the definitely repeated push and pull treatment vis-a-vis the indefinitely repeated treatment. While the Defection for the finitely repeated treatment reaches 66% by round 3, the indefinitely repeated game never exceeds 50% except for those games that reached round 7 and remains relatively stable across periods with a slight increase towards the later periods (bearing in mind that sample sizes decrease in the latter rounds). The difference is noticeable, and we can observe that indefinitely repeated games in fact provide a ground for mutual cooperation in the prisoner’s dilemma.
Conclusion
We have reviewed the theoretical predictions for the prisoner’s dilemma and the data outcomes for our Push & Pull adaptation. The data suggests that finitely repeated games are not able to support sustained cooperation, though higher levels of cooperation are observed than predicted by theory. Consistent with the theory, indefinitely repeated interactions are better at producing cooperative outcomes among students.
Overall, the theory predicts the outcomes presented by the data reasonably well and gives us hope of a practical kind. A mental shift for all of humanity towards seeing human interaction as an intergenerational push and pull game will produce a better outcome of cooperation for all of us in a vast variety of social dilemmas.
For further large-scale analysis of our experimental data, you can read up on our work or stay tuned for further posts coming up in this “Pulling back our curtains” series.
Want to see if your students will cooperate or defect? Get in touch with our team! We are eager to set it up for your class!
Push & Pull - Set Up
The Push & Pull game is an adaptation of the prisoner’s dilemma by Jim Andreoni & Hal Varian (1999). Instead of a classic matrix game, students are presented with two cards that they can play in which they either push a relatively higher reward to the other player or pull a relatively lower reward to themselves.

Figure 1. Game Interface with Action Set
The Problem
The prisoner’s dilemma occurs when two (or more) actors are faced with the same two choices: one choice leads to an overall better payoff for the group and each individual member (e.g. 2 * $400 for each if both Push); the other, actors have an individual incentive to defect (e.g. 2 * $300 for each) since they are individually better off to deviate regardless of whether the other actor cooperates or defects. This logic depicts many strategic situations such as arms races, doping in sports competitions, advertisement bidding, etc.
The interesting question is how do we overcome this dilemma?
Solution I - Repeated Interaction
One commonly proposed solution to this issue is repeated interaction. When trying to prevent an arms race, you can think of countries trying to tie themselves together in trade agreements, mutual cultural exchange, etc. to facilitate this kind of repeated interaction. However, theorists point out that repeated interaction in and of itself is not sufficient to sustain cooperation. Why is this? Well, if we suppose that the interactions last for say 5 rounds, the last round can be thought of as a simple one-round interaction since it is known that there is no next round taking place. That means the participants are incentivized to choose to defect. Given this knowledge, they should also defect in round 4 and you can see that this logic applies all the way to the first interaction, and the hope of cooperation is lost. But how does this theory hold up against the data in our treasure chest? We took all games which were played for 5 rounds and analyzed the mutual cooperation at the group level. That gives us N = 9004 observations.

Figure 2. Definitely Repeated Interaction
Solution II - Indefinite Repetition
But what if the actors don’t know when the repeated interaction will end? That is, if they do not know when the interaction with the other actors will end, they might be able to sustain cooperation. The logic derives from the fact that if the actors do not know when the interaction will end, the gain from momentarily defecting is outweighed by the potential loss of no future cooperation. Based on this, we would predict that we should observe higher levels of cooperation. We were able to retrieve N=1054 pairings from our database that played this game for at 3 rounds in the definite repetition treatment and N=3372 pairings in the indefinitely repetition treatment (50% probability that the game continues after round 3). Let’s look at what we can find concerning defection and cooperation.

Figure 3. Percent Defect, By Round
Conclusion
We have reviewed the theoretical predictions for the prisoner’s dilemma and the data outcomes for our Push & Pull adaptation. The data suggests that finitely repeated games are not able to support sustained cooperation, though higher levels of cooperation are observed than predicted by theory. Consistent with the theory, indefinitely repeated interactions are better at producing cooperative outcomes among students.
Overall, the theory predicts the outcomes presented by the data reasonably well and gives us hope of a practical kind. A mental shift for all of humanity towards seeing human interaction as an intergenerational push and pull game will produce a better outcome of cooperation for all of us in a vast variety of social dilemmas.
For further large-scale analysis of our experimental data, you can read up on our work or stay tuned for further posts coming up in this “Pulling back our curtains” series.
Want to see if your students will cooperate or defect? Get in touch with our team! We are eager to set it up for your class!

