With many news articles and social media posts highlighting “quiet quitting” and unionization efforts recently, labor market dynamics are in the public spotlight. For those who have not yet been exposed to the term, per Investopedia:
“Quiet quitting refers to doing the minimum requirements of one’s job and putting in no more time, effort, or enthusiasm than absolutely necessary. As such, it is something of a misnomer, since the worker doesn’t actually leave their position and continues to collect a salary.”
Incidentally, concepts related to the workplace can often be reasoned with game theory. MobLab’s Minimum Effort Game is a great way to teach the intuition of game theory, allows students to experience the risks associated with miscoordination in a simulated workplace, and if you choose to link this to quiet quitting, opens the classroom discussion to quiet quitting and how one individual’s reduced effort impacts the rest of the team.

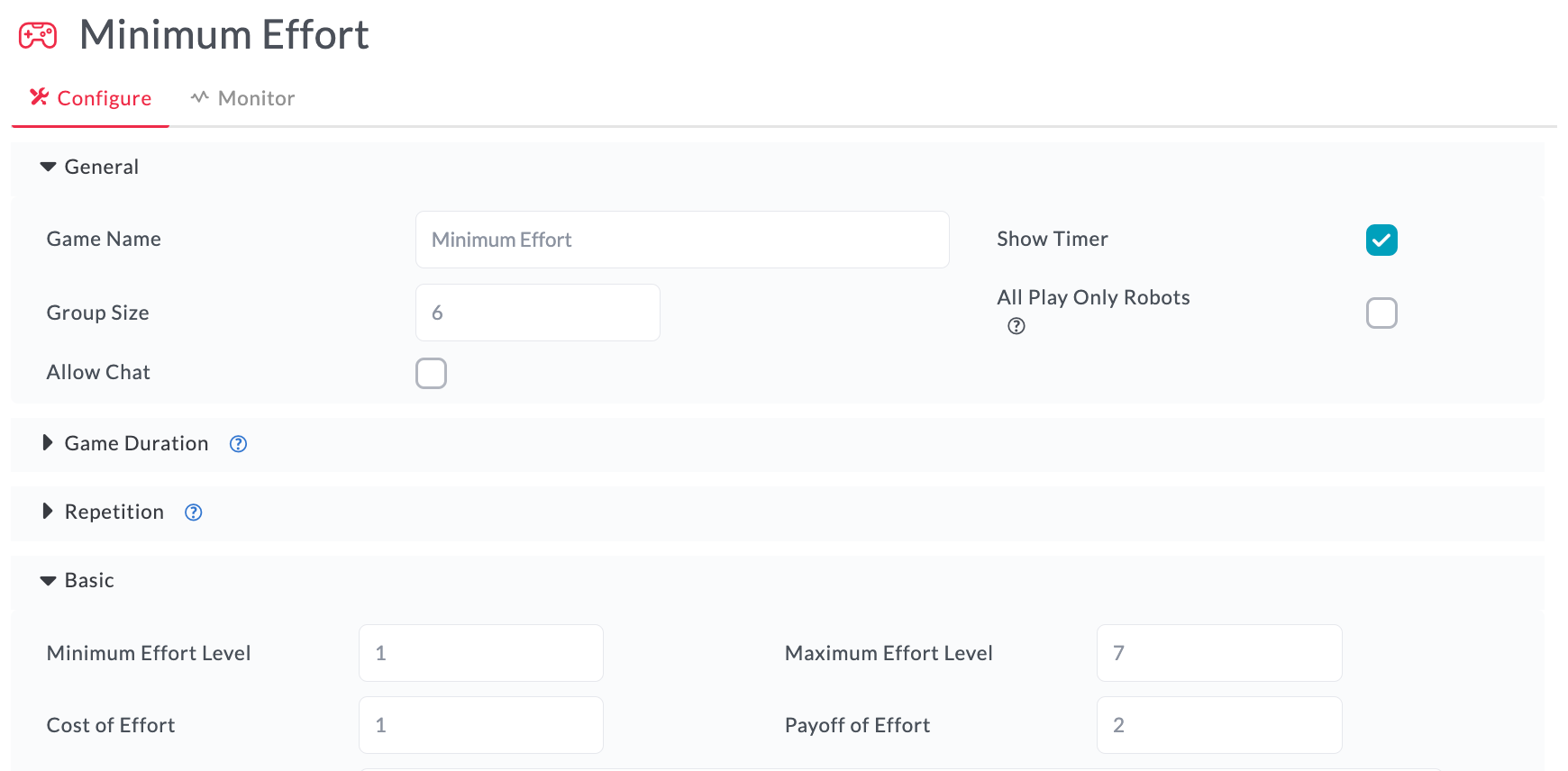
In the Minimum Effort game, students are in a group and play the workplace role of airline employees preparing a plane for takeoff. Each group member receives a bonus proportional to the number of minutes saved. In each round, they each choose how many minutes to save, and pay a cost proportional for their choice. Choices are then revealed, and the actual time saved is the smallest choice made by a group member - hence, minimum effort. Specifically, minimum effort refers to effort to reduce the amount of time to prepare the plane. The default parameters of the game shown in the MobLab instructor console screenshot below are:
Group size - we recommend 6 as a good group size for to introduce this strategic game Effort range - each group member chooses an effort level between Minimum Effort Level=1 and Maximum Effort Level=7 Payoff settings - Individuals pay a $1 per unit of effort they choose (Cost of Effort), and each receives a bonus per minute actually saved (Payoff of Effort) of $2 (where minutes actually saved equals the minimum effort chosen by a member of the group).
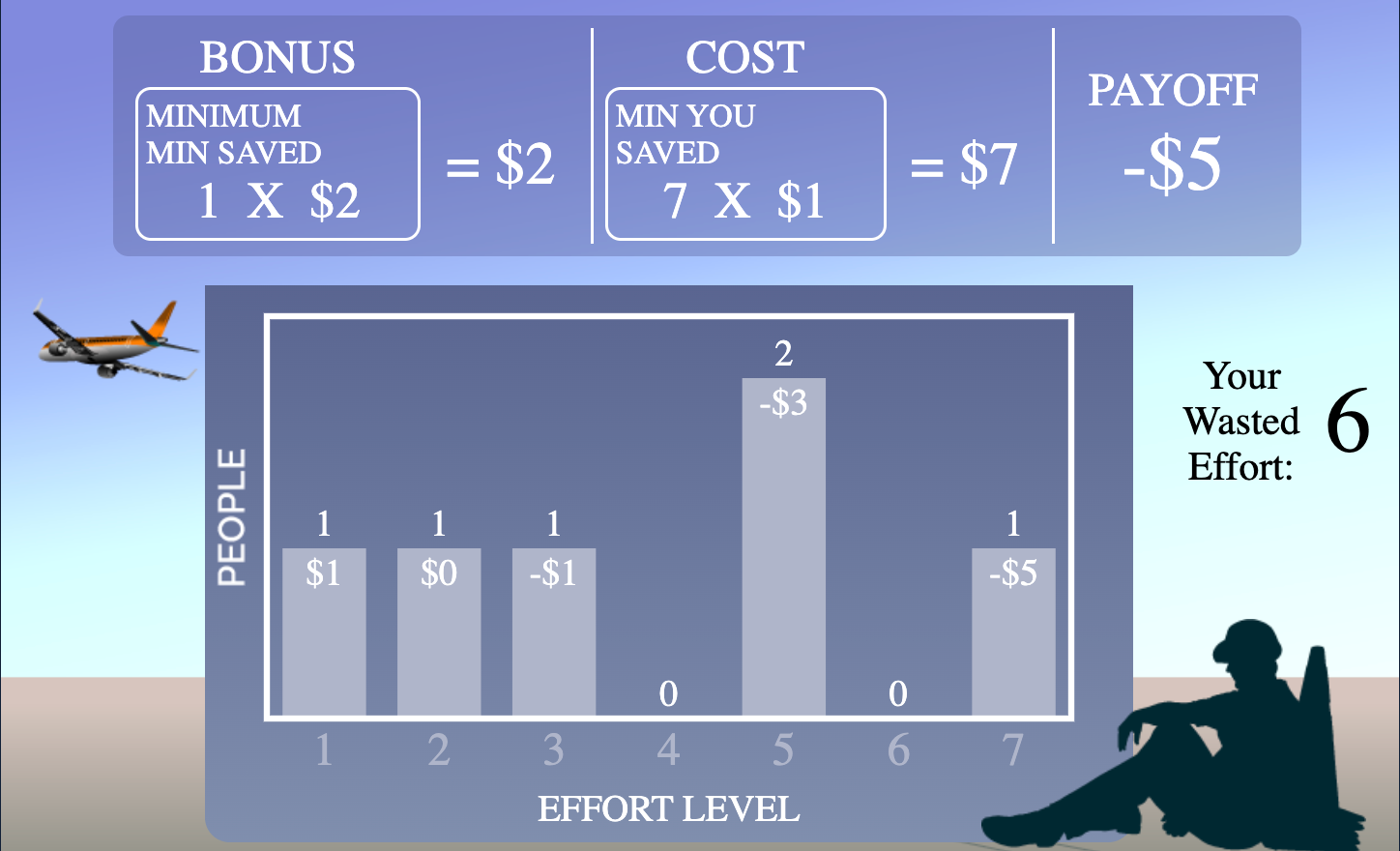
Below is an example of how player payoffs are computed. A player saved 4 minutes (effort) and the group members saved 3, 6, 4, 5 and 7 minutes (their individual efforts). Thus, the minimum effort is the lowest effort of the group (i.e., 3).

Now, let’s say a group member is incentivized to be put in the maximum effort out of the group. What result could happen from a game theory perspective? In any pure-strategy equilibrium, each group member chooses the same level of effort, and coordinating on any effort level is an equilibrium. Choosing the Maximum Effort Level is the payoff-dominant equilibrium.
However, a single player’s decision to choose maximization of effort for their own benefit is not devoid of risk for that player, especially if they work within a miscoordinated group. In other words, individual maximization does not always guarantee optimization within a given system (e.g., a network or group), especially if it is miscoordinated. Choosing the Maximum Effort Level (7 minutes in this case) exposes the player to the worst possible outcome if another group member happens to choose 1 for effort, which behaviorally can be interpreted as “quiet quitting.” As can been seen in the example, the player faces a -$5 payoff despite putting in maximum effort. What will the player decide next time? The player may put in less effort next time, which spreads the trend of quiet quitting.
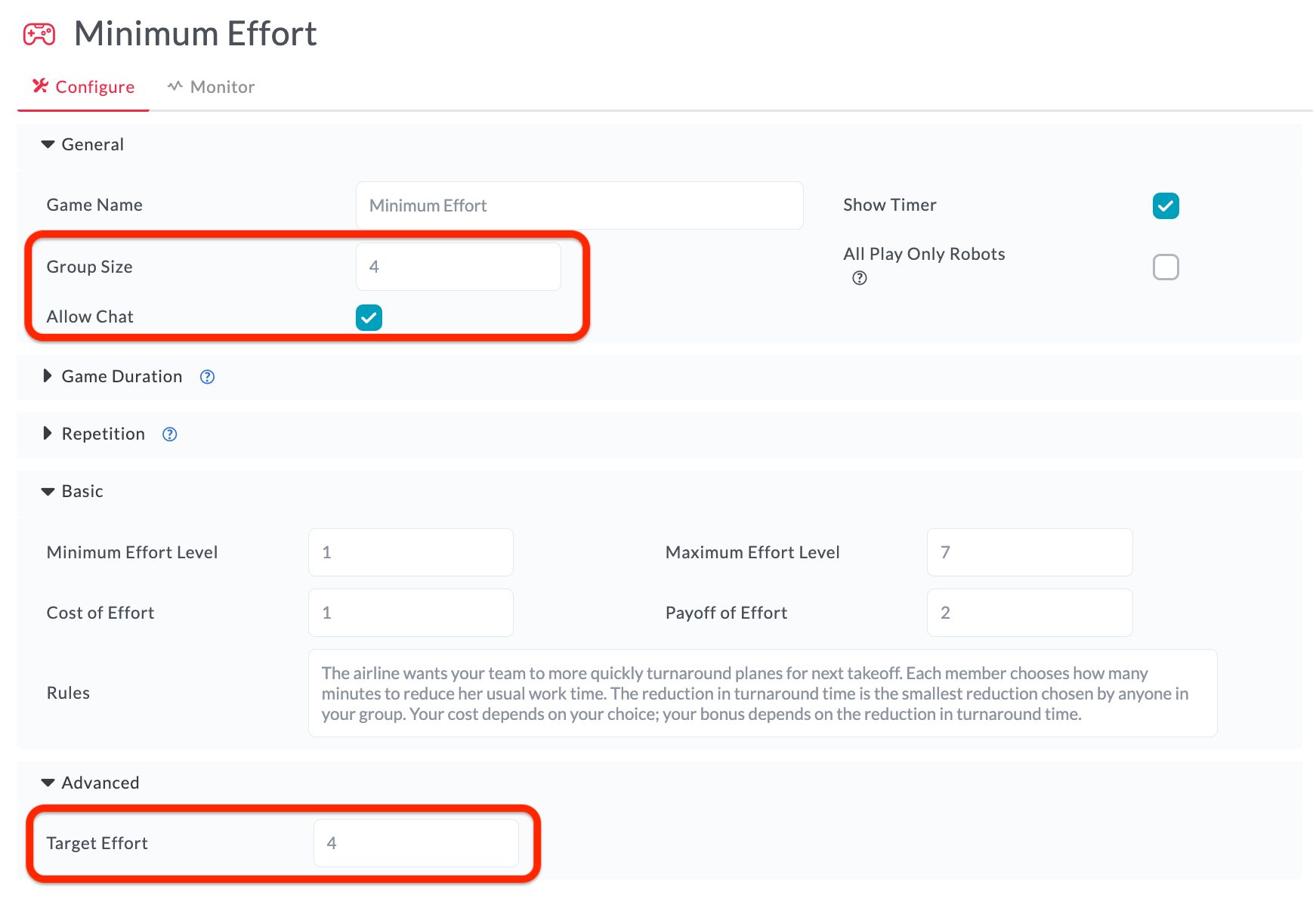
How can maximum effort and coordination be increased to help lower player risk of negative payoffs? Three options will likely increase coordination on higher levels of effort. The first is to allow group members to communicate by enabling chat. Second, you can have an effort-level target announced to each group member. To do so, change Target Effort from 0 to the desired target. Finally, smaller groups will have more minutes saved (on average). Decreasing Groups Size works in two ways. Splitting any group will likely result in one subgroup having a larger minimum than the original group, and students might respond with an increase in effort.
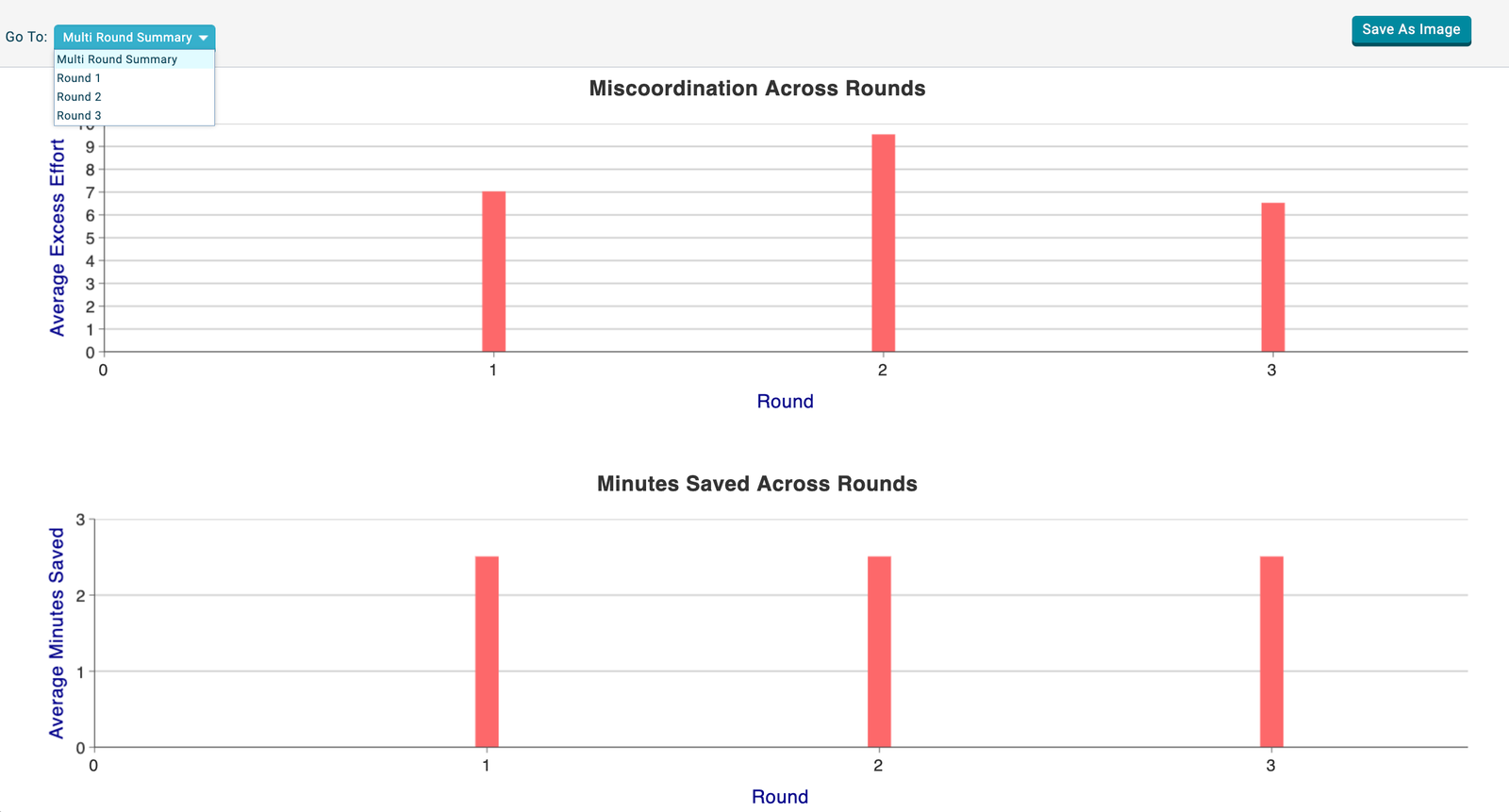
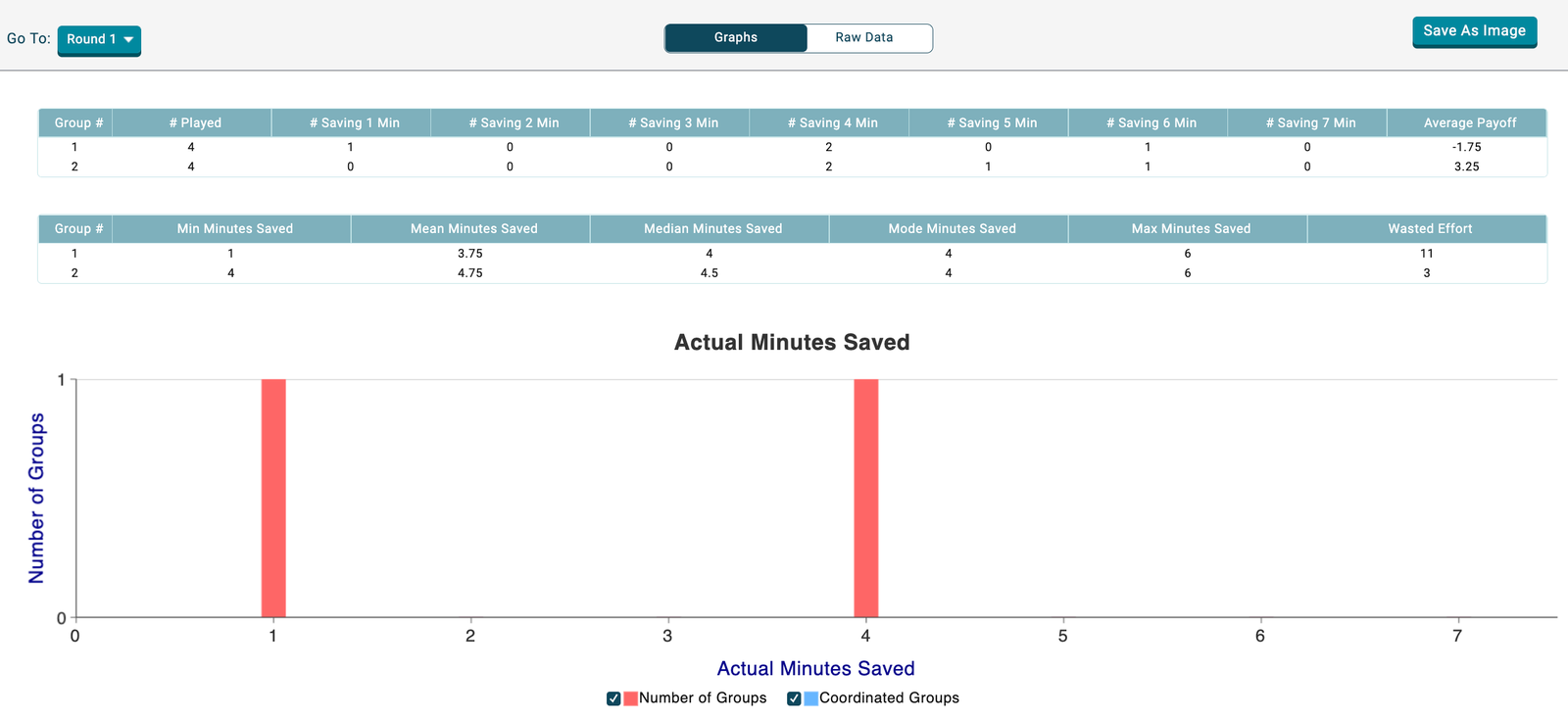
Game results can be shown in graphical and within-round summary tables. The results screen shows per-group (mis)coordination in a particular round as well as the trend across rounds. To switch between rounds, and the across-round summary, use the drop down menu at the upper-left of the results screen.
The concept of “quiet quitting” is not a new paradigm in labor markets and has been highlighted by game theory economists within different types of networks for quite some time. However, what is a new paradigm in teaching both game theory concepts and labor markets is MobLab’s Minimum Effort game. Now, you and your students can experience fun interactive simulations of current trending socioeconomic topics… all without feeling the need to quietly quit.
Want to see more interactive simulations of labor markets and game theory on our platform in action, like our Principal-Agent game? Get in touch and we would be happy to give you a personalized tour of the MobLab economics game platform.
“Quiet quitting refers to doing the minimum requirements of one’s job and putting in no more time, effort, or enthusiasm than absolutely necessary. As such, it is something of a misnomer, since the worker doesn’t actually leave their position and continues to collect a salary.”
Incidentally, concepts related to the workplace can often be reasoned with game theory. MobLab’s Minimum Effort Game is a great way to teach the intuition of game theory, allows students to experience the risks associated with miscoordination in a simulated workplace, and if you choose to link this to quiet quitting, opens the classroom discussion to quiet quitting and how one individual’s reduced effort impacts the rest of the team.

Will this flight depart on time or early? That will depend entirely on how much effort each group member provides!
In the Minimum Effort game, students are in a group and play the workplace role of airline employees preparing a plane for takeoff. Each group member receives a bonus proportional to the number of minutes saved. In each round, they each choose how many minutes to save, and pay a cost proportional for their choice. Choices are then revealed, and the actual time saved is the smallest choice made by a group member - hence, minimum effort. Specifically, minimum effort refers to effort to reduce the amount of time to prepare the plane. The default parameters of the game shown in the MobLab instructor console screenshot below are:

Default settings of the Minimum Effort game
Below is an example of how player payoffs are computed. A player saved 4 minutes (effort) and the group members saved 3, 6, 4, 5 and 7 minutes (their individual efforts). Thus, the minimum effort is the lowest effort of the group (i.e., 3).

Now, let’s say a group member is incentivized to be put in the maximum effort out of the group. What result could happen from a game theory perspective? In any pure-strategy equilibrium, each group member chooses the same level of effort, and coordinating on any effort level is an equilibrium. Choosing the Maximum Effort Level is the payoff-dominant equilibrium.
However, a single player’s decision to choose maximization of effort for their own benefit is not devoid of risk for that player, especially if they work within a miscoordinated group. In other words, individual maximization does not always guarantee optimization within a given system (e.g., a network or group), especially if it is miscoordinated. Choosing the Maximum Effort Level (7 minutes in this case) exposes the player to the worst possible outcome if another group member happens to choose 1 for effort, which behaviorally can be interpreted as “quiet quitting.” As can been seen in the example, the player faces a -$5 payoff despite putting in maximum effort. What will the player decide next time? The player may put in less effort next time, which spreads the trend of quiet quitting.

Maximization effort (individual overachieving) is not devoid of payoff risk if other members in the group also choose the lowest effort possible. This can help explain some of the reasoning and aspects behind “Quiet Quitting.”
How can maximum effort and coordination be increased to help lower player risk of negative payoffs? Three options will likely increase coordination on higher levels of effort. The first is to allow group members to communicate by enabling chat. Second, you can have an effort-level target announced to each group member. To do so, change Target Effort from 0 to the desired target. Finally, smaller groups will have more minutes saved (on average). Decreasing Groups Size works in two ways. Splitting any group will likely result in one subgroup having a larger minimum than the original group, and students might respond with an increase in effort.

Changing parameters (boxed in red) to help lower player risk of negative payoffs while increasing coordinated group effort.
Game results can be shown in graphical and within-round summary tables. The results screen shows per-group (mis)coordination in a particular round as well as the trend across rounds. To switch between rounds, and the across-round summary, use the drop down menu at the upper-left of the results screen.

Game results summary screen showing per-group miscoordination across all rounds.

Within-round summary tables. This example is for Round 1.
The concept of “quiet quitting” is not a new paradigm in labor markets and has been highlighted by game theory economists within different types of networks for quite some time. However, what is a new paradigm in teaching both game theory concepts and labor markets is MobLab’s Minimum Effort game. Now, you and your students can experience fun interactive simulations of current trending socioeconomic topics… all without feeling the need to quietly quit.
Want to see more interactive simulations of labor markets and game theory on our platform in action, like our Principal-Agent game? Get in touch and we would be happy to give you a personalized tour of the MobLab economics game platform.

