MobLab is known for teaching economics, game theory, and political science but have you given MobLab some thought for your statistics lessons? In particular, for introducing Bayesian statistics, we got our Monty Hall game. This way you can spice up your Bayesian statistics while having your participants go through the famous game show problem of finding a prize behind one of three doors.
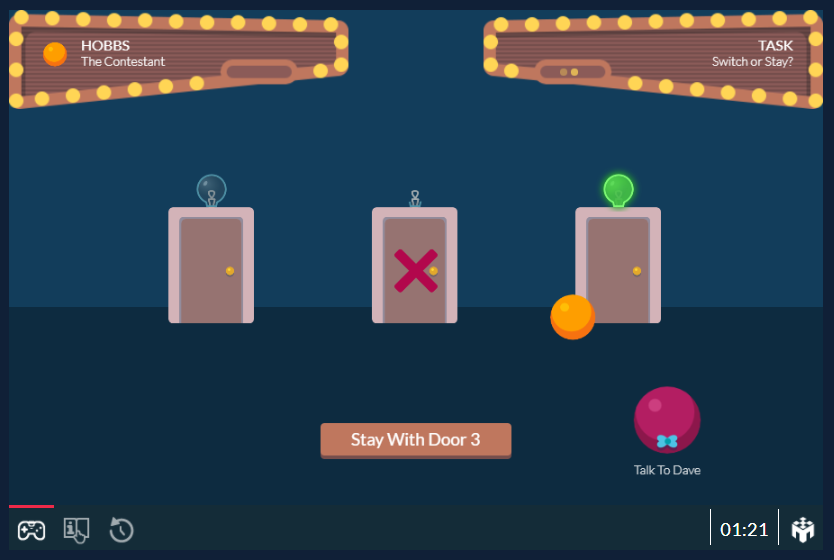
Monty Hall game interface
But let us provide a little bit of background as to why Bayesian Statistics should be taught. While once a controversial debate between the frequentists and Bayesian schools of statistics, it is now a universally accepted approach to statistical inference and people use both of them depending on the specific circumstances. Bayesian statistics has many applications in machine learning, financial forecasting, and in estimating so-called false positive or false negative probabilities. This is a particularly acute example to use in class to demonstrate how positive COVID cases can be more accurately estimated using a Bayesian approach.
Now onto our game: We have previously taken a look at Monty Hall but as a reminder, the game asks the contestant to choose one of three doors, where one prize is hiding. Then the game show host will open one of the other two doors showing that the prize is not behind it. Intuitively, people tend to stick with their original choice but using Bayes Rule, we can derive that switching the door after the host opens a dead-end door, doubles the odds of winning the price. The key insight to understanding this is that the opening of a door by the host provides additional information that should be used to update the probability of the prize being behind any given door. This idea tends to be unintuitive for students to grasp since we are used to the idea of a frequentist approach in which the new information of the second stage of the game has no influence on the probability of the car being behind any given door.
Enter the Monty Hall game - it provides you a tool to have your students test out the theory and experience how they will in fact more often obtain a prize by switching. Introducing Bayesian logic on another level, it is exactly the kind of data needed to update your students’ prior belief about the probability distribution of how to do well in this game.
After giving students some time, to try their luck at the doors, you can immediately debrief them in the classroom by using our results in the instructor console.

The first thing you will see is a summary table in our results section. Obviously, students in this class had some previous knowledge of this game and you can observe that about 2/3 of them switch in the second stage. It serves them well and they win at rates of 60-70% across rounds while students who do not switch win at rates of 22-33%. The difference is remarkably consistent and proves with only 77 participants over 3 rounds how the data confirms the (unintuitive) notion according to Bayes rule.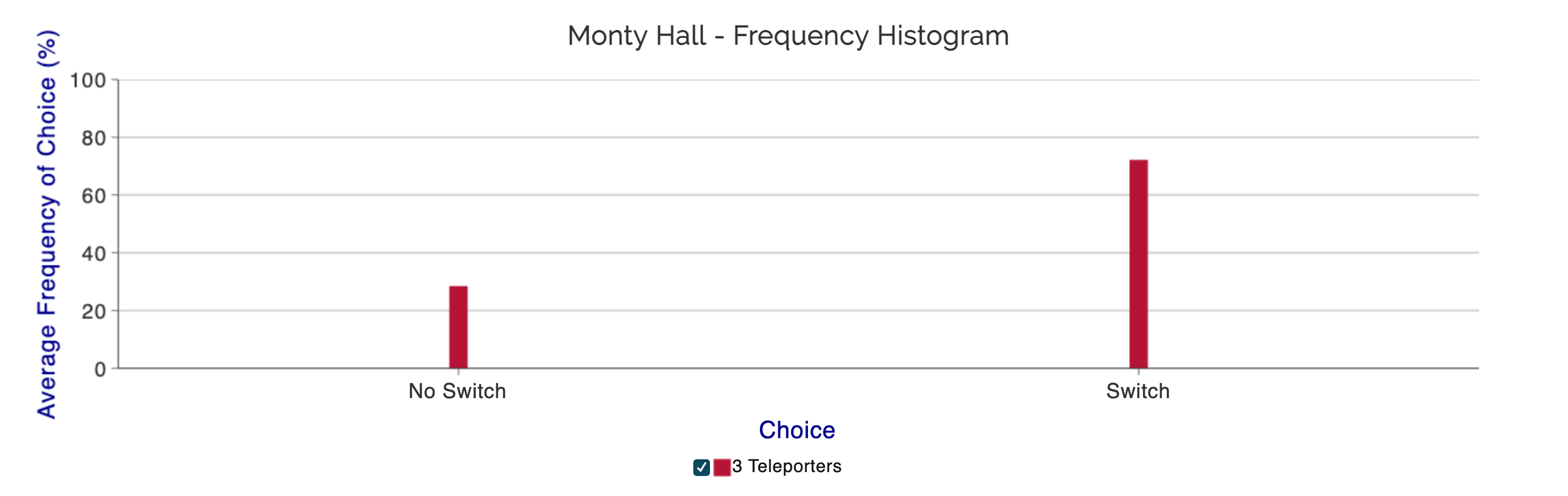
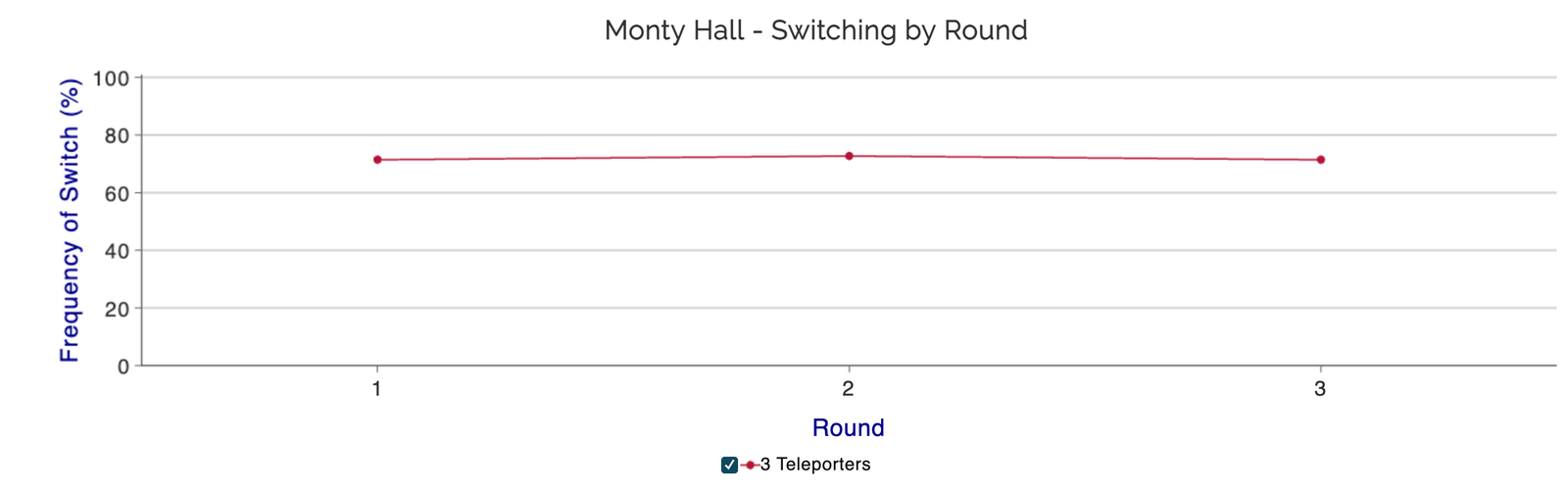
Below our summary table, you will find graphically displayed the average frequency of switching across rounds and the average count of Switch each round. Since these students had a high percentage of non-switchers from the start there is no trend observable despite the clearly better outcomes for the switchers. Of course, these cannot be observed by the individual in the game moving from round to round. In particular in repeated games, a trend should be expected as students experiment and notice better outcomes through switching.
If you prefer to take them out of the classical setting, MobLab has a second skin available in which students act as space explorers who have to obtain a teleporter to return home.
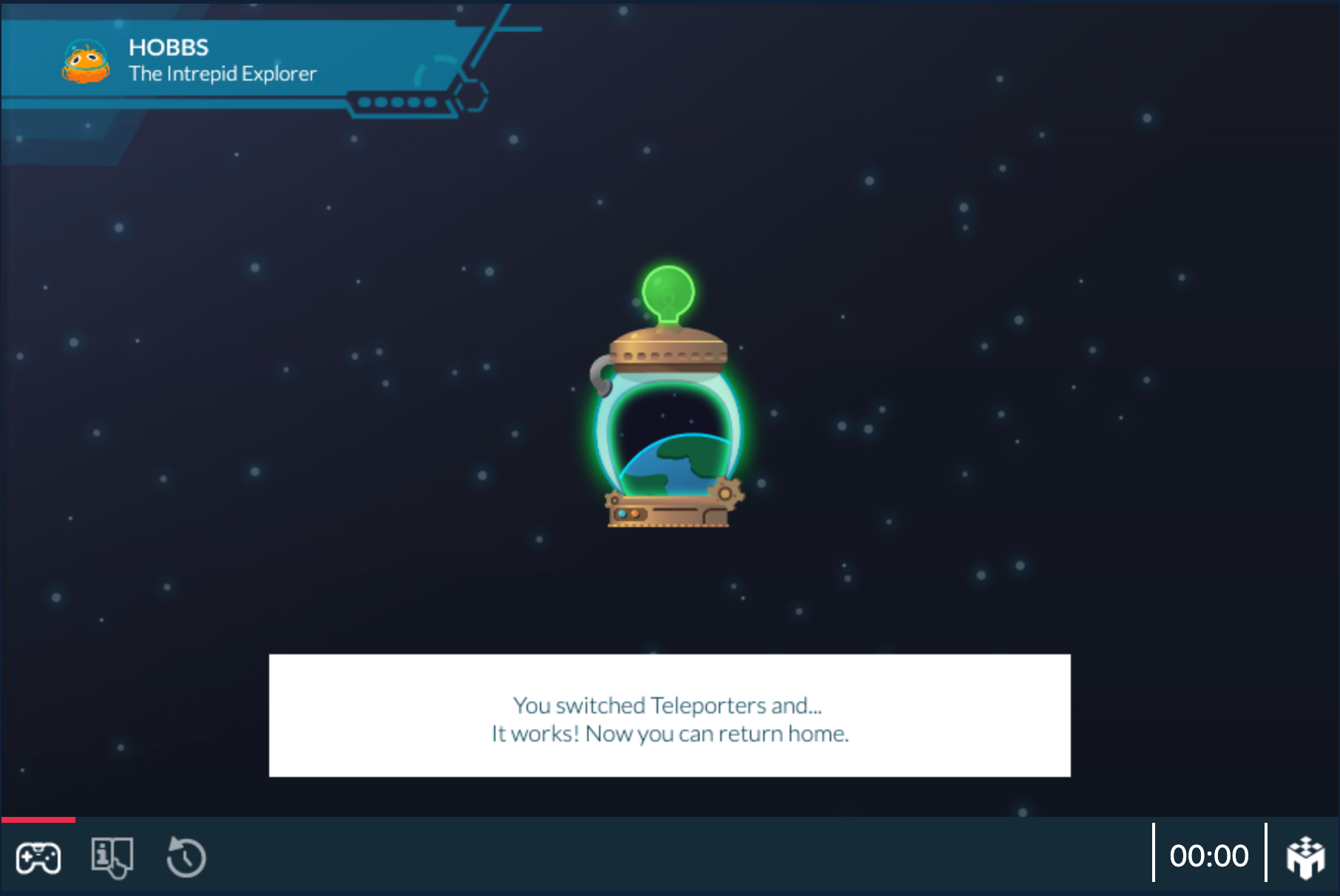
Alternative skin of Monty Hall game
If you would like to follow up the Monty Hall game with some exercises in calculating the probability of an event according to Bayes rule, we have a pre-built survey Bayesian Updating. The survey asks a series of questions in which students need to calculate the actual probability of an event given the information presented to them.
Bayesian Updating survey in the MobLab library
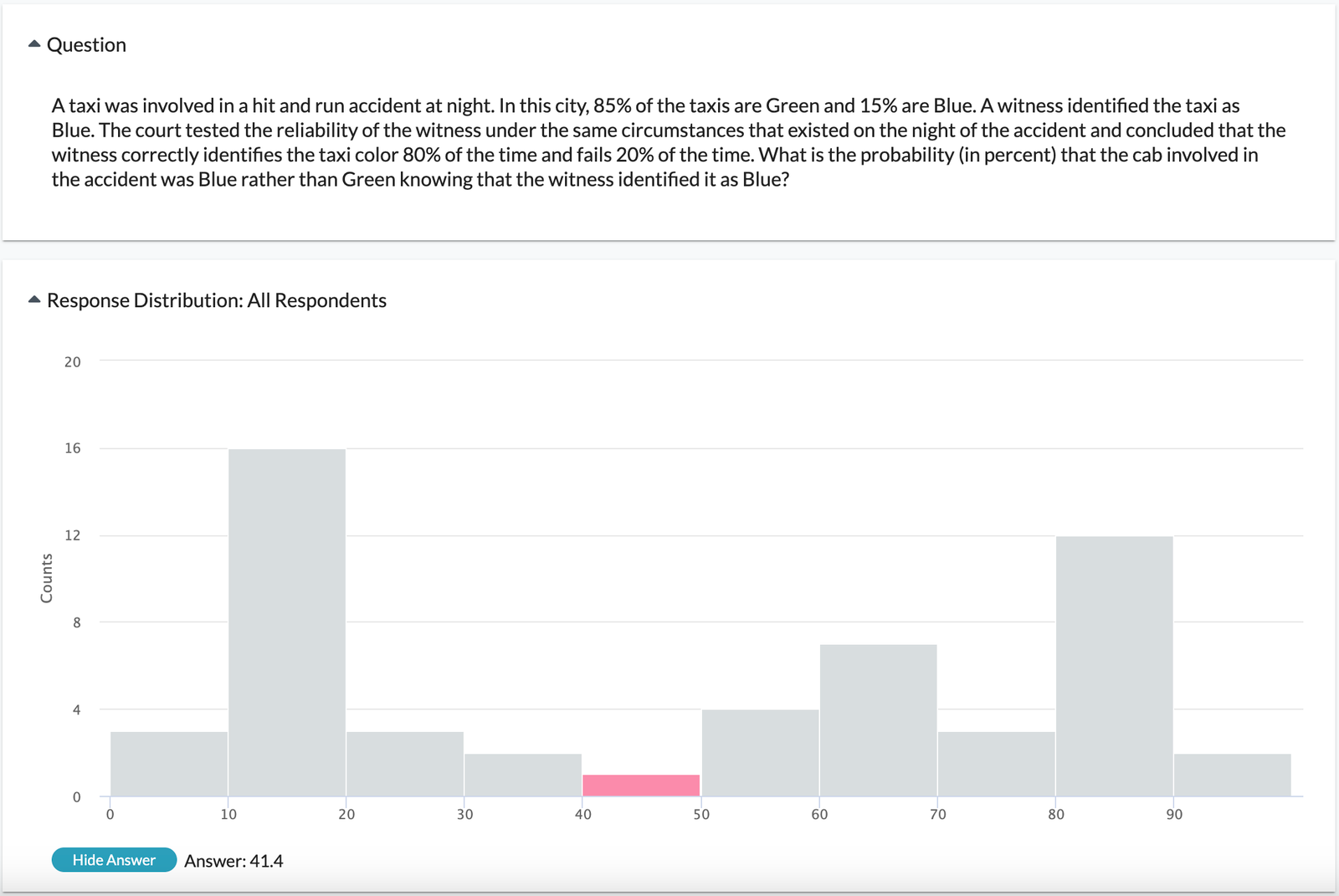
Sample question & results from Bayesian Updating survey
The survey questions highlight the effect on the estimates of such things as relative sample size of the observations and the strength of prior distributions versus observed outcomes. The sample question above exemplifies the latter by asking participants to calculate the probability that a cab involved in an accident was blue rather than green with a witness identifying the cab as blue. Given the information that most taxis in the city are green and the relatively high reliability of correct identification by witnesses (80%) students are often surprised to learn that in this case, the Bayesian approach yields a relatively low probability of the car being, in fact, blue. This is due to the strong nature of the prior knowledge, i.e. the distribution of the color of taxis in the city with 85% in favor of green. Thanks to our results feature you can immediately debrief your students on this visually, showing the response distribution in class and highlighting the correct result.
Bayesian Statistics has a variety of applications making it a very useful tool to teach to your students. It will help them understand concepts in machine learning as well as everyday life.
Would you like to learn more about MobLab economics games? Get in touch with our team. Schedule a personalized demo meeting with a MobLab team member.

Monty Hall game interface
But let us provide a little bit of background as to why Bayesian Statistics should be taught. While once a controversial debate between the frequentists and Bayesian schools of statistics, it is now a universally accepted approach to statistical inference and people use both of them depending on the specific circumstances. Bayesian statistics has many applications in machine learning, financial forecasting, and in estimating so-called false positive or false negative probabilities. This is a particularly acute example to use in class to demonstrate how positive COVID cases can be more accurately estimated using a Bayesian approach.
Now onto our game: We have previously taken a look at Monty Hall but as a reminder, the game asks the contestant to choose one of three doors, where one prize is hiding. Then the game show host will open one of the other two doors showing that the prize is not behind it. Intuitively, people tend to stick with their original choice but using Bayes Rule, we can derive that switching the door after the host opens a dead-end door, doubles the odds of winning the price. The key insight to understanding this is that the opening of a door by the host provides additional information that should be used to update the probability of the prize being behind any given door. This idea tends to be unintuitive for students to grasp since we are used to the idea of a frequentist approach in which the new information of the second stage of the game has no influence on the probability of the car being behind any given door.
Enter the Monty Hall game - it provides you a tool to have your students test out the theory and experience how they will in fact more often obtain a prize by switching. Introducing Bayesian logic on another level, it is exactly the kind of data needed to update your students’ prior belief about the probability distribution of how to do well in this game.
After giving students some time, to try their luck at the doors, you can immediately debrief them in the classroom by using our results in the instructor console.

Monty Hall Results Table
The first thing you will see is a summary table in our results section. Obviously, students in this class had some previous knowledge of this game and you can observe that about 2/3 of them switch in the second stage. It serves them well and they win at rates of 60-70% across rounds while students who do not switch win at rates of 22-33%. The difference is remarkably consistent and proves with only 77 participants over 3 rounds how the data confirms the (unintuitive) notion according to Bayes rule.

Depicting choices

Depicting choices across rounds
Below our summary table, you will find graphically displayed the average frequency of switching across rounds and the average count of Switch each round. Since these students had a high percentage of non-switchers from the start there is no trend observable despite the clearly better outcomes for the switchers. Of course, these cannot be observed by the individual in the game moving from round to round. In particular in repeated games, a trend should be expected as students experiment and notice better outcomes through switching.
If you prefer to take them out of the classical setting, MobLab has a second skin available in which students act as space explorers who have to obtain a teleporter to return home.

Alternative skin of Monty Hall game
If you would like to follow up the Monty Hall game with some exercises in calculating the probability of an event according to Bayes rule, we have a pre-built survey Bayesian Updating. The survey asks a series of questions in which students need to calculate the actual probability of an event given the information presented to them.

Bayesian Updating survey in the MobLab library

Sample question & results from Bayesian Updating survey
The survey questions highlight the effect on the estimates of such things as relative sample size of the observations and the strength of prior distributions versus observed outcomes. The sample question above exemplifies the latter by asking participants to calculate the probability that a cab involved in an accident was blue rather than green with a witness identifying the cab as blue. Given the information that most taxis in the city are green and the relatively high reliability of correct identification by witnesses (80%) students are often surprised to learn that in this case, the Bayesian approach yields a relatively low probability of the car being, in fact, blue. This is due to the strong nature of the prior knowledge, i.e. the distribution of the color of taxis in the city with 85% in favor of green. Thanks to our results feature you can immediately debrief your students on this visually, showing the response distribution in class and highlighting the correct result.
Bayesian Statistics has a variety of applications making it a very useful tool to teach to your students. It will help them understand concepts in machine learning as well as everyday life.
Would you like to learn more about MobLab economics games? Get in touch with our team. Schedule a personalized demo meeting with a MobLab team member.

