In the MobLab game Consumer Choice: Cobb-Douglas, students are introduced to the concept of optimal selection while constrained by a budget. The consumer choice game prompts students to choose between eating two types of sushi, which may have different respective prices, with a set budget. The students can see how many points (i.e. how much utility) each additional sushi provides. While playing the game, students know the utility from the next piece of each type and choose one piece at at time until the budget is depleted. The student’s goal while playing the game is to maximize the number of points. Playing over several rounds, students start to figure out that due to diminishing marginal utility, it is better to use their set budget to consume the sushi combination that brings them the most marginal utility.

Cobb Douglas Game Screen
The Consumer Choice game offers eight variations, with each round based on a variation of the Cobb-Douglas utility function:
How the optimal bundle responds to price and income changes The idea that a sushi roll's optimal budget share is equal to the ratio of its exponent to the sum of all exponents Student Results & Game Data
The end of game results highlight the optimal allocation of each type of sushi and how frequently your students followed the optimal decision rule. Showing students these game results helps them visualize and intuitively understand how their individual sushi decisions coincides with utility maximization according to the Cobb-Douglas model.

Figure 1: Outcome Across Problems
First, we present a table (Figure 1, above) which displays the percentage of students who maximized their utility (indicated here by the column % Answering Correctly).

Figure 2: Per-Problem Details Table
In the "Per-problem Details" section we show a summary table of each problem (Figure 2, above) and their optimal allocation of goods based on budget constraints. The optimal combination of Goods X and Y serve as a comparison point for your students and the allocation of goods they chose.
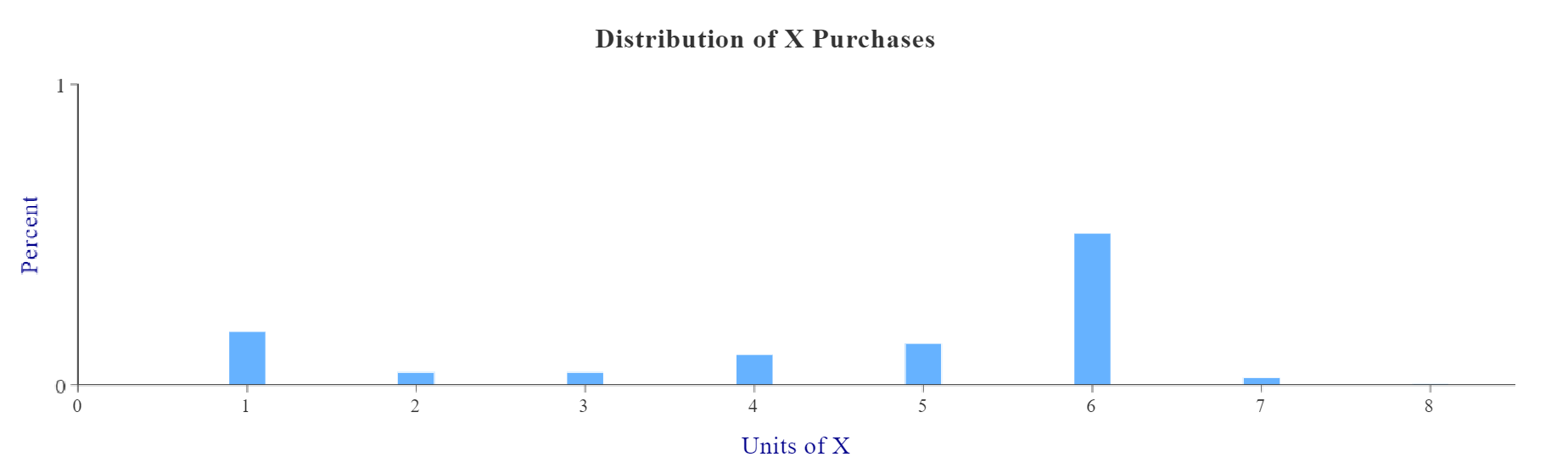
Figure 3: Distribution of Purchases
We then present a chart (Figure 3, above), showing how purchases of Good X are distributed in each problem. Ideally, the Optimal X allocation (6 units) should show the highest percentage across the distribution.
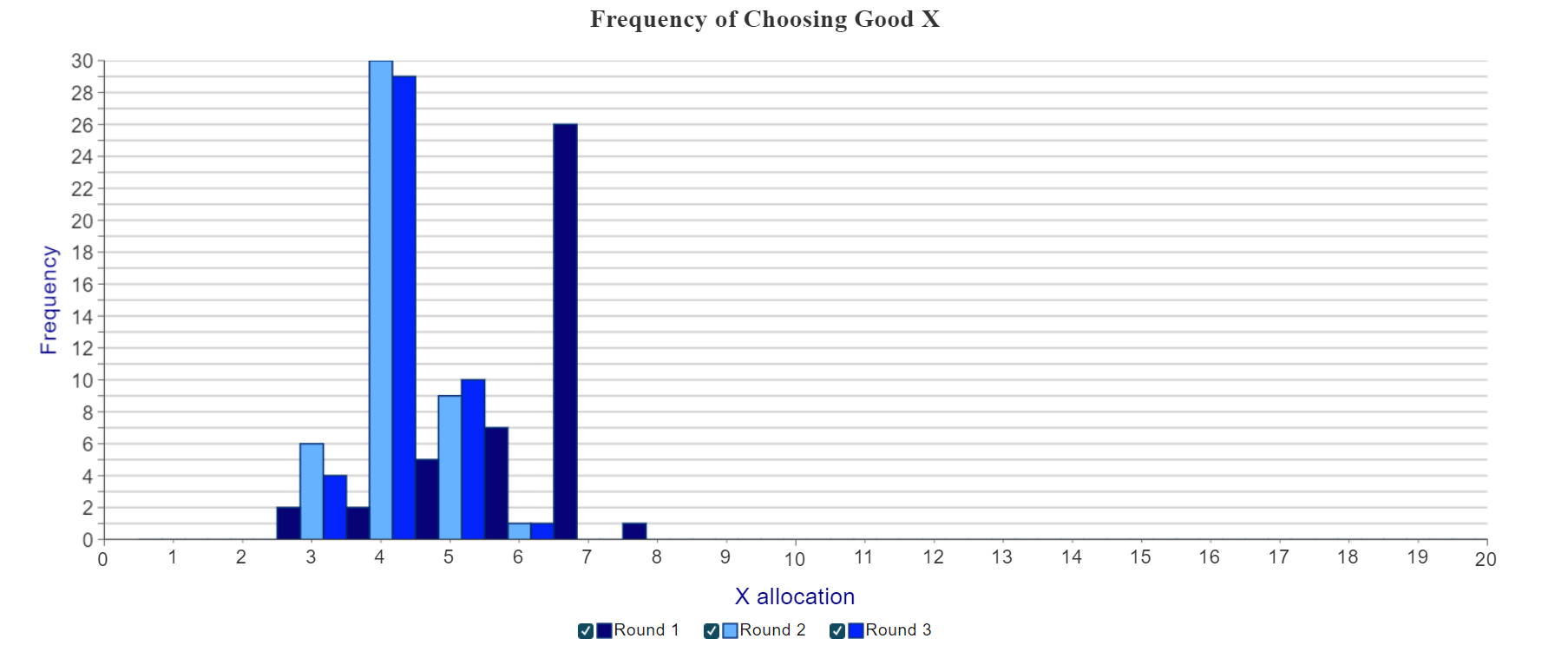
Figure 4: Frequency of Choices
Next, we present a graph showing the frequency of choices of Good X across all rounds played (Figure 4, above). Note that you can choose which round(s) to include in the graph by clicking on the checkboxes next to each item in the legend. Toggling between rounds can quantitatively illustrate to students differences in their consumption choices depending on the prices and Cobb Douglas function used in each round.
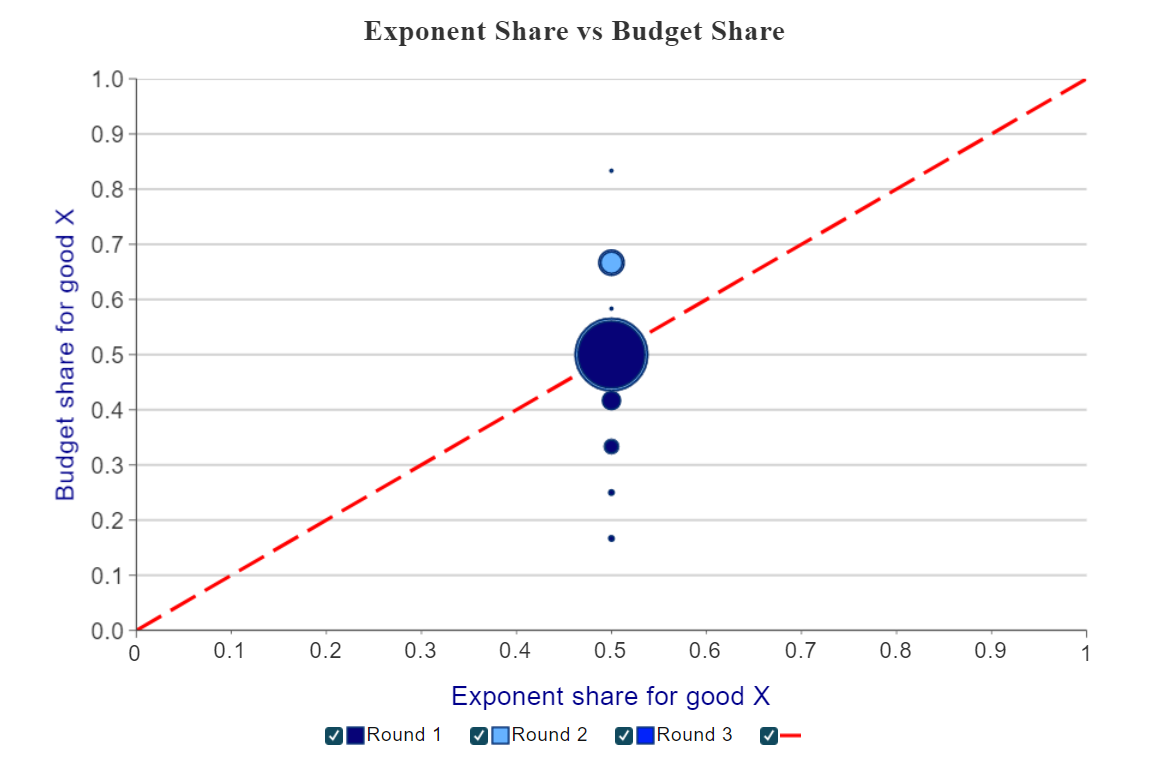
Figure 5: Exponent vs. Budget Share
Finally, we present a graph (Figure 5, above) showing the relationship between the exponent and budget share for Good X across rounds. A shaded circle is displayed for each round, with larger circles indicating a greater number of observations. When a student is maximizing utility, the budget share of Good X will be equal to the exponent share of Good X (shown by the dashed red line), which reiterates the idea that a sushi roll's optimal budget share is equal to the ratio of it's exponent to the sum of all exponents.
MobLab’s Cobb-Douglas game demonstrates and simplifies consumer preferences and utility functions in a really fun, intuitive way. This game also pairs great with others that you can explore in our MobLab Games Catalog.
Want to start playing and exploring MobLab online economics games on your own? Sign up for a free instructor account or get in touch with our team to schedule a one-on-one demo meeting. With just a few clicks, you can teach with MobLab games in-class or asynchronously.

Cobb Douglas Game Screen
u(x, y) = xa * y1 - a where 0 < a < 1
Each of the eight variations is designed to teach students certain aspects of maximization with Cobb-Douglas functions, such as:The end of game results highlight the optimal allocation of each type of sushi and how frequently your students followed the optimal decision rule. Showing students these game results helps them visualize and intuitively understand how their individual sushi decisions coincides with utility maximization according to the Cobb-Douglas model.

Figure 1: Outcome Across Problems

Figure 2: Per-Problem Details Table

Figure 3: Distribution of Purchases

Figure 4: Frequency of Choices

Figure 5: Exponent vs. Budget Share
MobLab’s Cobb-Douglas game demonstrates and simplifies consumer preferences and utility functions in a really fun, intuitive way. This game also pairs great with others that you can explore in our MobLab Games Catalog.
Want to start playing and exploring MobLab online economics games on your own? Sign up for a free instructor account or get in touch with our team to schedule a one-on-one demo meeting. With just a few clicks, you can teach with MobLab games in-class or asynchronously.

